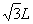题目内容
如图,![]() OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(
OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(![]() ,0),在
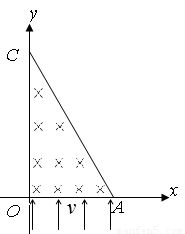
,0),在![]() OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
(1)求磁场的磁感应强度B的大小;
(2)若从OA边两个不同位置射入磁场的粒子,先后从OC边上的同一点P(P点图中未标出)射出磁场,求这两个粒子在磁场中运动的时间t1与t2之间应满足的关系;
(3)从OC边上的同一点P射出磁场的这两个粒子经过P点的时间间隔与P点位置有关,若该时间间隔最大值为![]() ,求粒子进入磁场时的速度大小。
,求粒子进入磁场时的速度大小。
解:(1) 粒子在t0时间内,速度方向改变了90°,故周期
T=4t0 ![]() (2分)
(2分)
由T=![]() 得B=
得B=![]()
![]() (2分)
(2分)
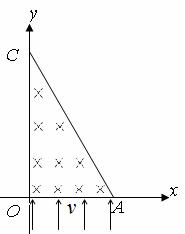
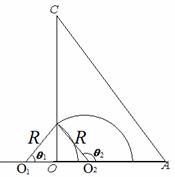
(2)在同一点射出磁场的两粒子轨迹如图,轨迹所对应的圆心角分别为![]() 和
和![]() ,由几何关系有
,由几何关系有
![]() =180°-
=180°-![]()
![]() (2分)
(2分)
故t1+ t2=![]() =2t0
=2t0 ![]() (1分)
(1分)
(3)由圆周运动知识可知,两粒子在磁场中运动的时间差![]() t与
t与![]() =
=![]() -
-![]() 成正比,由
成正比,由![]() 得
得
![]() =
=![]() -
-![]() =2
=2![]() -180°
-180° ![]() (1分)
(1分)
根据![]() 式可知
式可知![]() 越大,时间差
越大,时间差![]() t越大
t越大
由![]() t=
t=![]()
![]() (1分)
(1分)
由![]()
![]() 代入数据得
代入数据得![]() 的最大值为
的最大值为![]() =150°
=150° ![]() (1分)
(1分)
在磁场中运动时间最长的粒子轨迹如图,由几何关系![]() =30° ⑧(1分)
=30° ⑧(1分)
tan∠A=![]() =
=![]() 得∠A=60° ⑨
得∠A=60° ⑨
![]() =90°-∠A=30° ⑩ (1分)
=90°-∠A=30° ⑩ (1分)
![]() =L
=L ![]() (2分)
(2分)
解得R=![]()
![]() (1分)
(1分)
根据qvB=![]() (或v=
(或v=![]() 或v=
或v=![]() 均可)
均可) ![]() (2分)
(2分)
代入数据解得 v=![]()
![]() (1分)
(1分)

练习册系列答案
相关题目
 如图所示,三个相同的光滑曲面固定在同一竖直线的不同高度,曲面末端切线水平.三个相同的小球置于曲面的顶端,不计空气阻力( )
如图所示,三个相同的光滑曲面固定在同一竖直线的不同高度,曲面末端切线水平.三个相同的小球置于曲面的顶端,不计空气阻力( )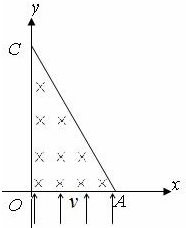 如图,△OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(
如图,△OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(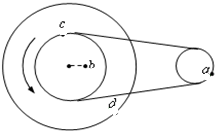 如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,试求:
如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,试求: