题目内容
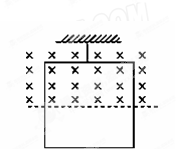
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小均为B的匀强磁场区域,区域I的磁场方向垂直斜面向上,区域II的磁场方向垂直斜面向下,磁场宽度HP及PN均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时刻ab边刚越过GH进入磁场I区域,此时导线框恰好以速度v1做匀速直线运动;t2时刻ab边下滑到JP与MN的中间位置,此时导线框又恰好以速度v2做匀速直线运动。重力加速度为g,下列说法中正确的是( )
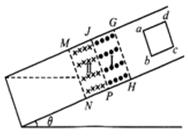

| A.当ab边刚越过JP时,导线框的加速度大小为a=gsinθ |
| B.导线框两次匀速直线运动的速度v1:v2=4:1 |
| C.从t1到t2的过程中,导线框克服安培力做功的大小等于重力势能的减少 |
D.从t1到t2的过程中,有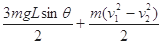 机械能转化为电能 机械能转化为电能 |
BD
试题分析:ab边刚越过GH进入磁场I区域时,电动势E1=BLv1,电流
 ,线框做匀速运动,所以
,线框做匀速运动,所以 ,当ab边刚越过JP时,电动势E2=2BLv1,
,当ab边刚越过JP时,电动势E2=2BLv1,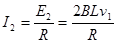 ,根据牛顿第二定律
,根据牛顿第二定律 ,联立解得a=3gsinθ,所以A错误;当a=0时,以速度v2做匀速直线运动,即
,联立解得a=3gsinθ,所以A错误;当a=0时,以速度v2做匀速直线运动,即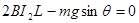 ,得:
,得: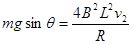 ,所以v1:v2=4:1,故B正确;从t1到t2的过程中,根据能量守恒导线框克服安培力做功的大小等于重力势能的减少加上动能的减少量,即克服安培力做功W=
,所以v1:v2=4:1,故B正确;从t1到t2的过程中,根据能量守恒导线框克服安培力做功的大小等于重力势能的减少加上动能的减少量,即克服安培力做功W=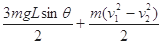 ,所以C错误;又克服安培力做功等于产生的电能,所以D正确。
,所以C错误;又克服安培力做功等于产生的电能,所以D正确。
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
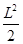

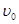 沿着导轨做匀速直线运动。在y轴的右方有一磁感应强度为B2的方向垂直纸面向外的匀强磁场,在x轴的下方有一场强为E的方向平行x轴向右的匀强电场。现有一质量为m、电荷量为q的带正电粒子在M板由静止经过平行金属板MN,然后以垂直于y轴的方向从F处沿直线穿过y轴,而后从x轴上的G处以与x轴正向夹角为60°的方向进入电场和磁场叠加的区域,最后到达y轴上的H点。已知OG长为l,不计粒子的重力。求:
沿着导轨做匀速直线运动。在y轴的右方有一磁感应强度为B2的方向垂直纸面向外的匀强磁场,在x轴的下方有一场强为E的方向平行x轴向右的匀强电场。现有一质量为m、电荷量为q的带正电粒子在M板由静止经过平行金属板MN,然后以垂直于y轴的方向从F处沿直线穿过y轴,而后从x轴上的G处以与x轴正向夹角为60°的方向进入电场和磁场叠加的区域,最后到达y轴上的H点。已知OG长为l,不计粒子的重力。求: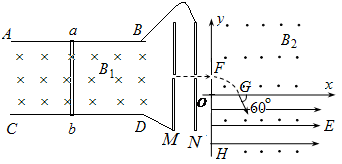
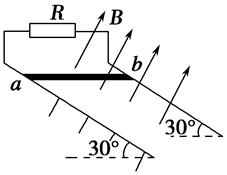
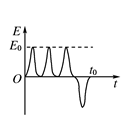
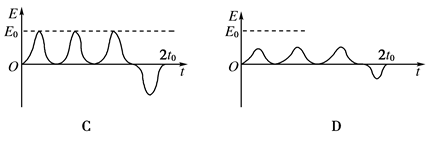
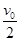 ,线圈中的E-t关系图可能是( )
,线圈中的E-t关系图可能是( )

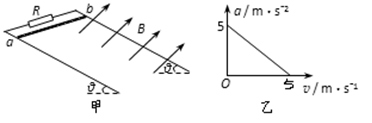
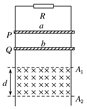
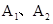 间有与导轨平面垂直的匀强磁场B,磁场区域的高度为d=0.3 m.导体棒a的质量ma=0.2 kg,电阻Ra=3 Ω;导体棒b的质量mb=0.1 kg,电阻Rb=6 Ω.它们分别从图中P、Q处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当b刚穿出磁场时a正好进入磁场.设重力加速度为g=10 m/s2,不计a、b之间的作用,整个过程中a、b棒始终与金属导轨接触良好,导轨电阻忽略不计.求:
间有与导轨平面垂直的匀强磁场B,磁场区域的高度为d=0.3 m.导体棒a的质量ma=0.2 kg,电阻Ra=3 Ω;导体棒b的质量mb=0.1 kg,电阻Rb=6 Ω.它们分别从图中P、Q处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当b刚穿出磁场时a正好进入磁场.设重力加速度为g=10 m/s2,不计a、b之间的作用,整个过程中a、b棒始终与金属导轨接触良好,导轨电阻忽略不计.求: