题目内容
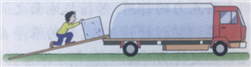
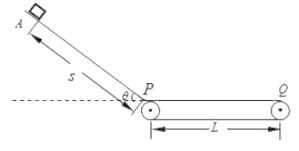
【题目】图所示,一倾角θ=37°的粗糙斜面底端与一传送带左端平滑相连于P点。有一可视为质点的物块从斜面顶端A点静止开始下滑,当物块滑到斜面底端P点后会继续滑上传送带(设经过P点前后的速度大小不变)。已知斜面长度S=1.25m,传动带长度L=4m,物块与斜面的动摩擦因数μ1=0.3,物块与传送带间的动摩擦因数μ2=0.2.(g取10m/s2,sin 37°=0.6,cos 37°=0.8),求:
(1)当传送带静止不动时,物块在传送带能滑行多远距离;
(2)当传送带以恒定速率v=4m/s逆时针转动时,试判断物体能否向右滑离出传动带?若能,试求出滑离速度;若不能,则求出物体在传送带上第一次做往返运动的总时间。
【答案】(2)2.25m;(3)3s
【解析】
(1)从A到P匀加速过程,根据牛顿第二定律有:
mgsin37°-μ1mgcos37°=ma1①
下滑到P点时的速度:
vp2=2a1s②
得
vp=3m/s
当传送带静止时:物块做匀减速运动,由牛顿第二定律得:
μ2mg=ma2③
减速到速度为零过程中位移大小为s0,由
0-vP2=-2a2s0④
解得:
s0=2.25m
故在传送带上滑行的最远距离为2.25m.
(2)当传送带以v=4m/s逆时针转动时,物块滑上传送带后仍做匀减速运动。
由(2)可知向右减速为零过程位移s0=2.25m<L,故物块不能从向右滑离出传送带。
设物块向右匀减速至速度为零的时间为 t1,则
0=vp-a2t1⑤
解得
t1=1.5s
物块反向匀加速到P点的时间为t2,则由运动对称性可知
t2=t1=1.5s
故物块在传送带上第一次做往返运动的总时间为
t=t1+t2=3s

 阅读快车系列答案
阅读快车系列答案【题目】某同学测量一段长度已知的电阻丝的电阻率.实验操作如下:
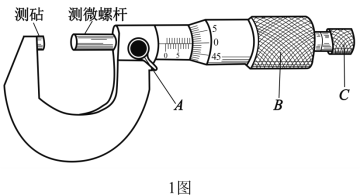
(1)螺旋测微器如题1图所示.在测量电阻丝直径时,先将电阻丝轻轻地夹在测砧与测微螺杆之间,再旋动_____(选填“A”“B”或“C”),直到听见“喀喀”的声音,以保证压力适当,同时防止螺旋测微器的损坏.
(2)选择电阻丝的_____(选填“同一”或“不同”)位置进行多次测量,取其平均值作为电阻丝的直径.
(3)2图甲中Rx,为待测电阻丝.请用笔画线代替导线,将滑动变阻器接入2图乙实物电路中的正确位置____
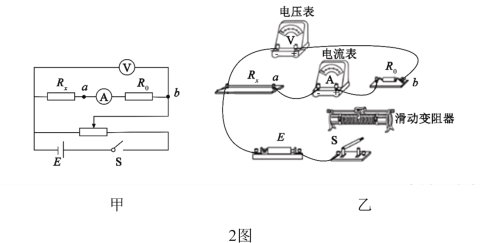
(4)为测量R,利用2图甲所示的电路,调节滑动变阻器测得5组电压U1和电流I1的值,作出的U1–I1关系图象如图图所示.接着,将电压表改接在a、b两端,测得5组电压U2和电流I2的值,数据见下表:
U2/V | 0.50 | 1.02 | 1.54 | 2.05 | 2.55 |
I2/mA | 20.0 | 40.0 | 60.0 | 80.0 | 100.0 |
请根据表中的数据,在方格纸上作出U2–I2图象.___
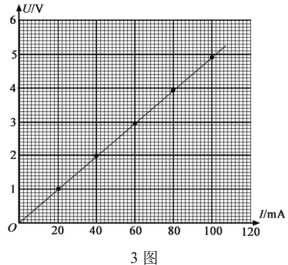
(5)由此,可求得电阻丝的Rx=______Ω.根据电阻定律可得到电阻丝的电阻率.