题目内容
14. 如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )
如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )| A. | 0°<θ<30° | B. | 0°≤θ≤30° | C. | 30°≤θ<45° | D. | 30°≤θ<60° |
分析 作出光路图,根据光的折射定律结合光在另一侧面上折射时不能发生全反射,通过几何关系求出顶角的范围.
解答 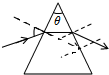 解:设入射光线经玻璃折射时,入射角为i,折射角为r,射至棱镜右侧面的入射角为α,根据折射定律得,
解:设入射光线经玻璃折射时,入射角为i,折射角为r,射至棱镜右侧面的入射角为α,根据折射定律得,
sini=nsinr ①
由几何关系得,
θ=α+r ②
当i=0时,由①知r=0,α有最大值αm.由②知,
θ=αm.③
同时αm应小于玻璃对空气全反射的临界角.即
sinαm<$\frac{1}{n}$=$\frac{1}{2}$,即 αm<30° ④
由①②③④式及题设条件可知 0<θ<30°.
故选:A
点评 解决本题的关键掌握光的折射定律,以及掌握发生全反射的条件和临界角公式 sinC=$\frac{1}{n}$.

练习册系列答案
相关题目
4.在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步.下列表述符合物理学史实的是( )
| A. | 普朗克为了解释黑体辐射现象,第一次提出了能量量子化理论 | |
| B. | 爱因斯坦为了解释光电效应的规律,提出了光子说 | |
| C. | 卢瑟福通过对α粒子散射实验的研究,提出了原子的核式结构模型 | |
| D. | 贝克勒尔通过对天然放射性的研究,发现原子核是由质子和中子组成的 | |
| E. | 玻尔大胆提出假设,认为实物粒子也具有波动性 |
9. 如图,质量为M的绝热活塞把一定质量的理想气体密封在竖直放置的绝热气缸内.活塞可在气缸内无摩擦滑动.现通过电热丝对理想气体十分缓慢地加热.设气缸处在大气中,大气压强恒定.经过一段较长时间后,下列说法正确的( )
如图,质量为M的绝热活塞把一定质量的理想气体密封在竖直放置的绝热气缸内.活塞可在气缸内无摩擦滑动.现通过电热丝对理想气体十分缓慢地加热.设气缸处在大气中,大气压强恒定.经过一段较长时间后,下列说法正确的( )
 如图,质量为M的绝热活塞把一定质量的理想气体密封在竖直放置的绝热气缸内.活塞可在气缸内无摩擦滑动.现通过电热丝对理想气体十分缓慢地加热.设气缸处在大气中,大气压强恒定.经过一段较长时间后,下列说法正确的( )
如图,质量为M的绝热活塞把一定质量的理想气体密封在竖直放置的绝热气缸内.活塞可在气缸内无摩擦滑动.现通过电热丝对理想气体十分缓慢地加热.设气缸处在大气中,大气压强恒定.经过一段较长时间后,下列说法正确的( )| A. | 气缸中气体的压强比加热前要大 | |
| B. | 气缸中气体的压强保持不变 | |
| C. | 气缸中气体的体积比加热前要少 | |
| D. | 气缸中气体的内能可能和加热前一样大 |
6.${\;}_{92}^{235}$U原子核在中子的轰击下发生一种可能的裂变反应,其裂变方程为${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→X+${\;}_{38}^{94}$Sr+2${\;}_{0}^{1}$n,则下列说法正确的是( )
| A. | X的原子核中含有141个核子 | |
| B. | X的原子核中含有86个中子 | |
| C. | 因为裂变释放能量,出现质量亏损,所以裂变后的总质量数减少 | |
| D. | 随着地球环境的不断变化,${\;}_{92}^{235}$U的半衰期可能变短也可能变长 |
4. 如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )
如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )
 如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )
如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )| A. | Ea>Eb;Fa>Fb | B. | Ea>Eb;Fa<Fb | C. | Ea<Eb;Fa<Fb | D. | Ea=Eb;Fa=Fb |

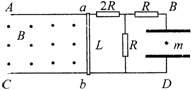 如图,在竖直面内有两平行金属导轨AB、CD.导轨间距为L,电阻不计.一根电阻不计的金属棒ab可在导轨上无摩擦地滑动.棒与导轨垂直,并接触良好.导轨之间有水平向外的匀强磁场,磁感强度为B.导轨右边与电路连接.电路中的三个定值电阻阻值分别为2R、R和R.在BD间接有一水平放置的平行板电容器C,板间距离为d.当ab棒以速度v0一直向左匀速运动时,在电容器正中心的质量为m的带电微粒恰好处于静止状态.
如图,在竖直面内有两平行金属导轨AB、CD.导轨间距为L,电阻不计.一根电阻不计的金属棒ab可在导轨上无摩擦地滑动.棒与导轨垂直,并接触良好.导轨之间有水平向外的匀强磁场,磁感强度为B.导轨右边与电路连接.电路中的三个定值电阻阻值分别为2R、R和R.在BD间接有一水平放置的平行板电容器C,板间距离为d.当ab棒以速度v0一直向左匀速运动时,在电容器正中心的质量为m的带电微粒恰好处于静止状态. 如图所示的直角坐标系中,在直线x=-2a到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴正方向,x轴下方的电场方向沿y轴负方向.一群电荷量为-q、质量为m的粒子被加速电压U0加速后,从电场左边界上A(-2a,a)到C(-2a,0)区域内,依次连续沿x轴正方向射入有界匀强电场.从A点射入的粒子,恰好从y轴上的A′(0,-a)沿x轴正方向射出有界匀强电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用
如图所示的直角坐标系中,在直线x=-2a到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴正方向,x轴下方的电场方向沿y轴负方向.一群电荷量为-q、质量为m的粒子被加速电压U0加速后,从电场左边界上A(-2a,a)到C(-2a,0)区域内,依次连续沿x轴正方向射入有界匀强电场.从A点射入的粒子,恰好从y轴上的A′(0,-a)沿x轴正方向射出有界匀强电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用