题目内容
3.苏联科学家齐奥尔科夫斯基提出了多级火箭的概念.把火箭一级一级的接在一起,三级火箭从上到下依次为运载物、第三级、第二级和第一级构成,实际应用中一般不会超过四级,可以简化成模型,运载物的质量为M,每一级的质量为m,当运载物和三级物离开地面时已经具有速度v0,点火过程连续,上次一点火后紧接着点火下一级(可以看成反冲现象),每一级物分离时速度大小均为$\frac{{v}_{0}}{2}$,每次分离时间t,M=3m忽略空气阻力,不考虑燃料消耗质量,重力加速度为g.(1)当第一级与火箭主体分离时,求火箭主体速度.
(2)最后一次分离运载物获得推力为多大.
分析 (1)火箭与运载物组成的系统动量守恒,应用动量守恒定律可以求出火箭主体的速度.
(2)对运载物,应用动量定理可以求出运载物获得的推力.
解答 解:(1)火箭分离过程系统动量守恒,以向上为正方向,由动量守恒定律得,
第一级分离时:(M+3m)v0=(M+2m)v1+m×$\frac{{v}_{0}}{2}$,解得:v1=$\frac{11}{10}$v0,
第二级分离时:(M+2m)v1=(M+m)v2+m×$\frac{{v}_{0}}{2}$,解得:v2=$\frac{5}{4}$v0,
第二级分离时:(M+m)v2=Mv3+m×$\frac{{v}_{0}}{2}$,解得:v3=$\frac{3}{2}$v0;
(2)对运载物,由动量定理得:Ft=Mv3-Mv2,解得:F=$\frac{3m{v}_{0}}{4t}$;
答:(1)当第一级与火箭主体分离时,火箭主体速度为$\frac{11}{10}$v0;
(2)最后一次分离运载物获得推力为$\frac{3m{v}_{0}}{4t}$.
点评 火箭分离时内力远大于外力,系统动量守恒,分析清火箭运动过程,应用动量守恒定律与动量定理可以解题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
13. 如图所示,放置在水平地面上的木板B的左端固定一轻弹簧,弹簧右端与物块A相连.已知A、B质量相等,二者处于静止状态,且所有接触面均光滑.现设法使物块A以一定的初速度沿木板B向右运动,在此后的运动过程中弹簧始终处在弹性限度内,且物块A始终在木板B上.下列说法中正确的是( )
如图所示,放置在水平地面上的木板B的左端固定一轻弹簧,弹簧右端与物块A相连.已知A、B质量相等,二者处于静止状态,且所有接触面均光滑.现设法使物块A以一定的初速度沿木板B向右运动,在此后的运动过程中弹簧始终处在弹性限度内,且物块A始终在木板B上.下列说法中正确的是( )
 如图所示,放置在水平地面上的木板B的左端固定一轻弹簧,弹簧右端与物块A相连.已知A、B质量相等,二者处于静止状态,且所有接触面均光滑.现设法使物块A以一定的初速度沿木板B向右运动,在此后的运动过程中弹簧始终处在弹性限度内,且物块A始终在木板B上.下列说法中正确的是( )
如图所示,放置在水平地面上的木板B的左端固定一轻弹簧,弹簧右端与物块A相连.已知A、B质量相等,二者处于静止状态,且所有接触面均光滑.现设法使物块A以一定的初速度沿木板B向右运动,在此后的运动过程中弹簧始终处在弹性限度内,且物块A始终在木板B上.下列说法中正确的是( )| A. | 物块A的加速度先减小后增大 | |
| B. | 物块A的速度最大时弹簧的弹性势能最大 | |
| C. | 木板B的速度最大时弹簧最长 | |
| D. | 木板B的速度最大时物块A的速度为零 |
14. 如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )
如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )
 如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )
如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )| A. | 0°<θ<30° | B. | 0°≤θ≤30° | C. | 30°≤θ<45° | D. | 30°≤θ<60° |
11.如图所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于木板向上、大小为F=8N的力作用下加速度与倾角的关系.已知物块的质量m=1kg,通过DIS实验,描绘出了如图(b)所示的加速度大小a与倾角θ的关系图线(θ<90°).若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2.则下列说法中正确的是( )
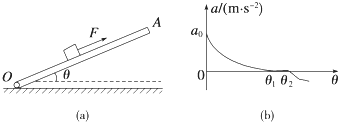

| A. | 由图象可知木板与水平面的夹角处于θ1和θ2之间时,物块所受摩擦力一定为零 | |
| B. | 由图象可知木板与水平面的夹角大于θ2时,物块所受摩擦力不一定沿木板向上 | |
| C. | 根据题意可以计算得出物块加速度a0的大小为6m/s2 | |
| D. | 根据题意可以计算当θ=45°时,物块所受摩擦力为Ff=μmgcos 45°=$\sqrt{2}$N |
18. 如图所示,实线表示两等量同种电荷的电场线,虚线MN为两点电荷连线的中垂线,虚线AB垂直于两点电荷的连线,A点离B点较近.两个相同的带负电的粒子分别从A、B两点以相同的初速度开始运动,速度方向垂直于MN,且都能经过如图所示的P点.设粒子在A、B两点的电势分别为φA和φB,电势能分别为EpA和EpB,以过 P点时的速度大小分别为vA和vB,到达P点经过的时间分别为tA和tB.粒子的重力不计,则( )
如图所示,实线表示两等量同种电荷的电场线,虚线MN为两点电荷连线的中垂线,虚线AB垂直于两点电荷的连线,A点离B点较近.两个相同的带负电的粒子分别从A、B两点以相同的初速度开始运动,速度方向垂直于MN,且都能经过如图所示的P点.设粒子在A、B两点的电势分别为φA和φB,电势能分别为EpA和EpB,以过 P点时的速度大小分别为vA和vB,到达P点经过的时间分别为tA和tB.粒子的重力不计,则( )
 如图所示,实线表示两等量同种电荷的电场线,虚线MN为两点电荷连线的中垂线,虚线AB垂直于两点电荷的连线,A点离B点较近.两个相同的带负电的粒子分别从A、B两点以相同的初速度开始运动,速度方向垂直于MN,且都能经过如图所示的P点.设粒子在A、B两点的电势分别为φA和φB,电势能分别为EpA和EpB,以过 P点时的速度大小分别为vA和vB,到达P点经过的时间分别为tA和tB.粒子的重力不计,则( )
如图所示,实线表示两等量同种电荷的电场线,虚线MN为两点电荷连线的中垂线,虚线AB垂直于两点电荷的连线,A点离B点较近.两个相同的带负电的粒子分别从A、B两点以相同的初速度开始运动,速度方向垂直于MN,且都能经过如图所示的P点.设粒子在A、B两点的电势分别为φA和φB,电势能分别为EpA和EpB,以过 P点时的速度大小分别为vA和vB,到达P点经过的时间分别为tA和tB.粒子的重力不计,则( )| A. | φA<φB | B. | EpA>EpB | C. | vA<vB | D. | tA>tB |
15.下列叙述符合物理学史实的是( )
| A. | 自然界的电荷只有两种,法拉第把它们命名为正电荷和负电荷 | |
| B. | 安培提出了分子电流假说,解释了磁铁的磁场和电流的磁场在本质上相同 | |
| C. | 库仑最早引入了电场概念,并提出用电场线表示电场 | |
| D. | 奥斯特对电磁感应现象的研究,将人类带人了电气化时代 |
12.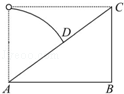 如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )
如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )
 如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )
如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )| A. | tanα | B. | 2tanα | C. | tan2α | D. | 2tan2α |
 如图所示,半径为R的绝缘光滑圆环固定在竖直平面内,环上套一质量为m且带正电荷的珠子,空间存在水平向右的匀强电场,珠子所受静电力是其重力的$\frac{3}{4}$倍,将珠子从环上最低位置A点静止释放.
如图所示,半径为R的绝缘光滑圆环固定在竖直平面内,环上套一质量为m且带正电荷的珠子,空间存在水平向右的匀强电场,珠子所受静电力是其重力的$\frac{3}{4}$倍,将珠子从环上最低位置A点静止释放.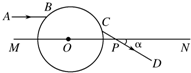 如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=$\sqrt{2}$,MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.
如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=$\sqrt{2}$,MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.