��Ŀ����
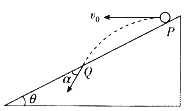
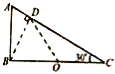
����Ŀ����3�֣���2014��̫ԭ���У����Ϊ30���ֱ�������εױ߳�Ϊ2L���ױߴ���ˮƽλ�ã�б��Ϊ�⻬��Ե���죬���ڵױ��е�O���̶�һ�����Q����һ������Ϊm�Ĵ������ʵ�q��б�涥��A��б���£�������б�棩����ͼ��ʾ���Ѳ��������B��б���ϵĴ���D��ʱ�ٶ�Ϊv�����ٶ�Ϊa��������б�����£�����ʵ㻬��б�ߵ�C��ʱ���ٶȺͼ��ٶȵ���ֵ�ֱ��ǣ� ��
A��![]() ��g��a B��
��g��a B��![]() ��a C��
��a C��![]() ��g��a D��
��g��a D��![]() ��a
��a
���𰸡�A
��������
������������ݼ���֪ʶ�����õ�B��C��D��������OΪԲ�ĵ�ͬһԲ���ϣ�����ĵ�����ȣ����q��D��C������ֻ���������������ݶ��ܶ�������ʵ㻬��б�ߵ�C��ʱ���ٶȣ������ʵ�q��C����������������ţ�ٵڶ����ɺͿ��ض�������ʵ㻬��б�ߵ�C��ʱ���ٶȣ�
�⣺���⣬BD��AC��O����BC���е㣬���ݼ���֪ʶ�õ�B��C��D��������OΪԲ�ĵ�ͬһԲ���ϣ������ڵ���Q�����ĵ糡���ǵ��Ƶ㣬���ԣ�q��D��C�Ĺ����е糡�е糡������Ϊ�㣮
�ɶ��ܶ����ã�mgh=![]()
��h=![]() =
=![]() ������vC=
������vC=![]()
�ʵ���D���������������ã��糡F��������Oָ��D�㣻����mg��������ֱ���£�֧����N������ֱ��б�����ϣ���ţ�ٵڶ����ɣ���
mgsin30�㩁Fcos30��=ma����
�ʵ���C�������������ã��糡F��������Oָ��C�㣻����mg��������ֱ���£�֧����N������ֱ��б�����ϣ���ţ�ٵڶ����ɣ���
mgsin30��+Fcos30��=maC����
�ɢ٢ڽ�ã�aC=g��a����A��ȷ��BCD����
��ѡ��A��

 ��ѧ�����ϵ�д�
��ѧ�����ϵ�д� �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�