题目内容
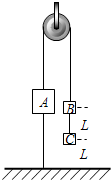 如图所示,物块A的质量为M,物块B、C的质量都是m,并都可看作质点,且m<M<2m.三物块用细线通过滑轮连接,物块B与物块C的距离和物块C到地面的距离都是L.现将物块A下方的细线剪断,若物块A距滑轮足够远且不计一切阻力.求:
如图所示,物块A的质量为M,物块B、C的质量都是m,并都可看作质点,且m<M<2m.三物块用细线通过滑轮连接,物块B与物块C的距离和物块C到地面的距离都是L.现将物块A下方的细线剪断,若物块A距滑轮足够远且不计一切阻力.求:(1)若B不能着地,求
| M | m |
(2)若B能着地,物块A距离最初位置上升的最大高度.
分析:(1)C落地后,根据AB两物体系统机械能守恒,求出B恰好落地的临界条件,再判断M与m的关系;
(2)物块B着地后,A做竖直上抛运动,根据运动学公式列式求解.
(2)物块B着地后,A做竖直上抛运动,根据运动学公式列式求解.
解答:解:(1)A、B、C三物块系统机械能守恒.B、C下降L,A上升L时,A的速度达最大.
2mgL-MgL=
(M+2m)V2,
解得:v=
当C着地后,若B恰能着地,即B物块下降L时速度为零.A、B两物体系统机
械能守恒.
MgL-mgL=
(M+m)V2
将V代入,整理得:M=
m所以
>
时,B物块将不会着地.
(2)若
<
,B物块着地,着地后A还会上升一段.设上升的高度为h,
B着地时A、B整体的速度大小为V1,从C着地至B着地过程中根据动能定理可得
-MgL+mgL=
(M+m)(V12-V2)
解得:V12=
B着地后A继续上升的高度h=
=
所以A 上升的最大高度H=2L+h=2L+
答:(1)若B不能着地,求
满足的条件为
>
;
(2)若B能着地,物块A距离最初位置上升的最大高度为2L+
.
2mgL-MgL=
| 1 |
| 2 |
解得:v=
|
当C着地后,若B恰能着地,即B物块下降L时速度为零.A、B两物体系统机
械能守恒.
MgL-mgL=
| 1 |
| 2 |
将V代入,整理得:M=
| 2 |
| M |
| m |
| 2 |
(2)若
| M |
| m |
| 2 |
B着地时A、B整体的速度大小为V1,从C着地至B着地过程中根据动能定理可得
-MgL+mgL=
| 1 |
| 2 |
解得:V12=
| 4(2m2-M2)gL |
| (m+M)(2m+M) |
B着地后A继续上升的高度h=
| V12 |
| 2g |
| 2(2m2-M2)L |
| (m+M)(2m+M) |
所以A 上升的最大高度H=2L+h=2L+
| 2(2m2-M2)L |
| (m+M)(2m+M) |
答:(1)若B不能着地,求
| M |
| m |
| M |
| m |
| 2 |
(2)若B能着地,物块A距离最初位置上升的最大高度为2L+
| 2(2m2-M2)L |
| (m+M)(2m+M) |
点评:本题关键是要灵活地选择研究对象,虽然单个物体机械能不守恒,但系统机械能守恒

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图所示,物块A的质量m=2kg,木板B长L=1m、质量M=3kg.开始时两物体静止,且物块A在木板B的最右端,现用F=24N的水平拉力拉着轻质滑轮水平向左运动,经过一段时间,物块A滑到木板的最左端,不计一切摩擦,求:
如图所示,物块A的质量m=2kg,木板B长L=1m、质量M=3kg.开始时两物体静止,且物块A在木板B的最右端,现用F=24N的水平拉力拉着轻质滑轮水平向左运动,经过一段时间,物块A滑到木板的最左端,不计一切摩擦,求: 如图所示,物块A的质量为m,物块B 的质量是M.且m<M.二物块用细线通过轻质滑轮连接,物块B 到地面的距离是l.现将物块A下方的细线剪断,A距滑轮足够远且不计一切阻力.求:物块A上升的最大高度?一位同学解题过程:设A上升的最大高度为h∵AB整体的机械能守恒最高点时AB的速度为零∴MgL=mgh∴h=ML/m
如图所示,物块A的质量为m,物块B 的质量是M.且m<M.二物块用细线通过轻质滑轮连接,物块B 到地面的距离是l.现将物块A下方的细线剪断,A距滑轮足够远且不计一切阻力.求:物块A上升的最大高度?一位同学解题过程:设A上升的最大高度为h∵AB整体的机械能守恒最高点时AB的速度为零∴MgL=mgh∴h=ML/m (2009?松江区二模)如图所示,物块A的质量为M,物块B、C 的质量都是m.且m<M<2m.三物块用细线通过轻质滑轮连接,物块B与物块C的距离和物块C到地面的距离都是l.现将物块A下方的细线剪断,A距滑轮足够远且不计一切阻力.求:
(2009?松江区二模)如图所示,物块A的质量为M,物块B、C 的质量都是m.且m<M<2m.三物块用细线通过轻质滑轮连接,物块B与物块C的距离和物块C到地面的距离都是l.现将物块A下方的细线剪断,A距滑轮足够远且不计一切阻力.求: