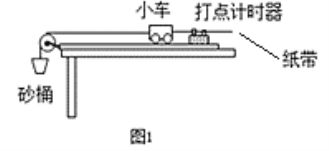
��Ŀ����
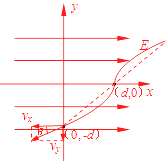
����Ŀ����ͼ��ʾ����ǿ�糡������x���������ǿΪE����A��d��0������һ����ֹ���������������ڲ����ã�ijһʱ��ͻȻ���ѳ�����������Ϊm�Ĵ����������е����Ϊq����1��y�Ḻ�����˶�������һ��ʱ�䵽�0����d���㣮���������ͷ��Ѻ�����������ã�����
��1������ʱ���������Ե��ٶȣ�
��2������1���0����d����ʱ���糡������1������˲�书�ʣ�
��3������1���0����d����ʱ��������ľ��룮
���𰸡�
��1���⣺��1��y����������������ֱ���˶�����x���������ܺ㶨�ĵ糡�������ȼ���ֱ���˶���������1��������ƽ���˶���
����1����ʱ���ٶ�Ϊv1����2���ٶ�Ϊv2���У�
��y��������
d=v1t
��x��������a= ![]() ��
��
d= ![]() at2
at2
v1= ![]()
�ٶȷ�����y��ĸ�����
���������ѳ�����ʱ�����ض����غ㶨�ɣ���
mv1+mv2=0
���� v2=��v1
���� v2�Ĵ�СΪ ![]() ��������y������
��������y������
�𣺷���ʱ��1���ٶȴ�СΪ ![]() ����������y��ĸ�������2���ٶȴ�СΪ
����������y��ĸ�������2���ٶȴ�СΪ ![]() ����������y���������
����������y���������
��2���⣺����1���0����d����ʱ���ٶ�ΪVB����糡��������˲ʱ����Ϊ��
P=qEVB cos��=qEVBx��
�������˶�ѧ��ʽ VBx= ![]() =
= ![]() ��
��
���� P=qE ![]() ��
��
�𣺵���1���0����d����ʱ���糡������1������˲�书���� qE ![]()
��3���⣺�������˶����жԳ��ԣ���ͼ��ʾ������1���0����d����ʱ������λ��
S1= ![]() d��
d��
����1���0����d����ʱ��������ľ���ΪBC=2S1=2 ![]() d��
d��
�𣺵���1���0����d����ʱ��������ľ�����2 ![]() d��
d��
����������1����1��������ƽ���˶���������ƽ���˶��Ĺ��ɿ��������1���ٶȵĴ�С�����ɶ����غ������2���ٶȵĴ�С����2���糡��������˲ʱ���ʣ�Ҫ���ص糡�������˲ʱ�ٶȵĴ�С������P=Fv�������˲ʱ���ʵĴ�С����3���������ӵ��˶��켣���ɼ���֪ʶ�������������ľ��룮