题目内容
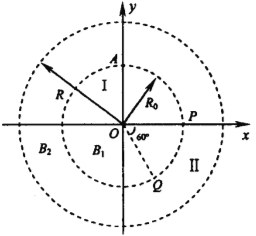
【题目】如图所示，在xOy平面内，0＜x＜2L的区域内有一方向竖直向上的匀强电场，2L＜x＜3L的区域内有一方向竖直向下的匀强电场，两电场强度大小相等。x＞3L的区域内有一方向垂直于xOy平面向外的匀强磁场。某时刻，一带正电的粒子从坐标原点以沿x轴正方向的初速度v0进入电场；之后的另一时刻，一带负电粒子以同样的初速度从坐标原点进入电场。正、负粒子从电场进入磁场时速度方向与电场和磁场边界的夹角分别为60°和30°，两粒子在磁场中分别运动半周后在某点相遇。已经两粒子的重力以及两粒子之间的相互作用都可忽略不计，两粒子带电量大小相等。求：
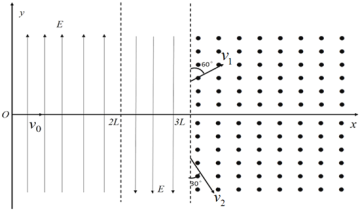
（1）正、负粒子的质量之比m1：m2；
（2）两粒子相遇的位置P点的坐标；
（3）两粒子先后进入电场的时间差。
【答案】（1）3:1（2）（6.5L，
）（3）
【解析】（1）设粒子初速度为
，进磁场方向与边界的夹角为θ。
①
记
，则粒子在第一个电场运动的时间为2t，在第二个电场运动的时间为t
②
③
由①②③得
所以
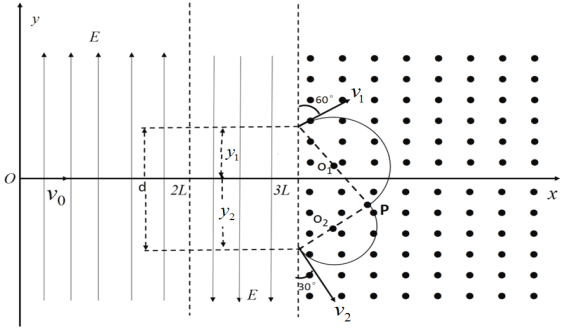
（2）正粒子在电场运动的总时间为3t
第一个t的竖直位移为
，第二个t的竖直位移为
，由对称性，第三个t的竖直位移为
，所以
结合①②得
同理
由几何关系，P点的坐标为
（3）设两粒子在磁场中运动半径为
、
由几何关系
两粒子在磁场中运动时间均为半个周期
由于两粒子在电场中运动时间相同，所以进电场时间差即为磁场中相遇前的时间差
解得
练习册系列答案
名校课堂系列答案
相关题目
