题目内容
【题目】如图所示，光滑绝缘的半圆形圆弧轨道ACD，固定在竖直面内，轨道处在垂直于轨道平面向里的匀强磁场中，半圆弧的直径AD水平，因弧的半径为R，匀强磁场的磁感应强度为B，在A端由静止释放一个带正电荷质量为m的金属小球甲，结果小球甲连续两次通过轨道最低点C时，对轨道的压力差为ΔF，小球运动过程始终不脱离轨道，重力加速度为g.求：
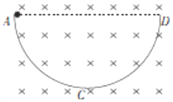
（1）小球甲经过轨道最低点C时的速度大小；
（2）小球甲所带的电量；
（3）若在圆弧轨道的最低点C放一个与小球甲完全相同的不带电的金属小球乙，让小球甲仍由轨道的A端由静止释放，则甲球与乙球发生弹性碰撞后的一瞬间，乙球对轨道的压力.（不计两球间静电力的作用）
【答案】（1）
（2）
（3）3mg-
，方向竖直向下
【解析】（1）由于小球甲在运动过程中，只有重力做功，因此机械能守恒，运动到C点时，
mgR=
mvC2
求得
（2）小球甲第一次通过C点时. 
第二次通过C点时
由题意知ΔF=F2-F1
求得
（3）因为甲球与乙球在最低点发生的是弹性碰撞，则
mvc=mv甲+ mv乙
求得v甲=0，v乙= vc
设碰撞后的一瞬间，轨道对乙的支持力大小为F乙，方向经直向上，则
求得F乙=3mg-
根据牛顿第三定律可知，此时球乙对轨道的压力大小为3mg-
，方向竖直向下
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
