题目内容
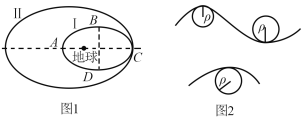
【题目】如图1所示,一质量为m的卫星绕地球在椭圆轨道Ⅰ上运转,运行周期为T0,轨道Ⅰ上的近地点A到地球球心的距离为a,远地点C到地球球心的距离为b,BD为椭圆轨道的短轴。A、C两点的曲率半径均为ka(通过该点和曲线上紧邻该点两侧的两点作一圆,在极限情况下,这个圆就叫做该点的曲率圆,如图2,其半径ρ叫做该点的曲率半径)。若地球的质量为M,引力常量为G。则
A.卫星在轨道Ⅰ上运行时的机械能等于在轨道Ⅱ上运行时的机械能
B.如果卫星要从轨道Ⅱ返回到轨道Ⅰ,则在C位置时动力气源要向后喷气
C.卫星在C→D→A的运动过程中,万有引力对其做的功为![]() GMmk(
GMmk(![]() –
–![]() )
)
D.卫星在C→D→A的运动过程中,万有引力对其做的功为![]() GMmk(
GMmk(![]() –
–![]() )
)
【答案】C
【解析】由题图1可知,卫星从轨道Ⅰ变轨到轨道Ⅱ,要有外力对卫星做功,所以卫星在轨道Ⅰ上的机械能小于其在轨道Ⅱ上的,A错误;若卫星要从轨道Ⅱ上的C位置变轨到轨道Ⅰ上,则在C位置时卫星要减速,动力气源要向前喷气,B错误;在A、C两点卫星的运动可近似看作半径为ka,速度分别为vA、vC的圆周运动,则有G![]() =m
=m![]() ,G
,G![]() =m
=m![]() ,在C→D→A过程中,由动能定理有W=
,在C→D→A过程中,由动能定理有W=![]() mvA2–
mvA2–![]() mvC2,解得W=
mvC2,解得W=![]() GMmk(
GMmk(![]() –
–![]() ),C正确,D错误。
),C正确,D错误。

练习册系列答案
相关题目