[题目]如图所示.竖直线MN∥PQ.MN与PQ间距离为a.其间存在垂直纸面向里的匀强磁场.磁感应强度为B.O是MN上一点.O处有一粒子源.某时刻放出大量速率均为v(方向均垂直磁场方向).比荷一定的带负电粒子(粒子重力及粒子间的相互作用力不计).已知沿图中与MN成θ=60°角射出的粒子恰好垂直PQ射出磁场.则粒子在磁场中运动的最长时间为:A 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，竖直线MN∥PQ，MN与PQ间距离为a，其间存在垂直纸面向里的匀强磁场，磁感应强度为B，O是MN上一点，O处有一粒子源，某时刻放出大量速率均为v(方向均垂直磁场方向)、比荷一定的带负电粒子(粒子重力及粒子间的相互作用力不计)，已知沿图中与MN成θ=60°角射出的粒子恰好垂直PQ射出磁场，则粒子在磁场中运动的最长时间为：

A. B. C. D.

【答案】C

【解析】当速度方向与MN夹角θ=60°时，粒子恰好垂直PQ方向射出磁场，所以，粒子运动的半径

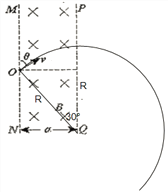
由粒子在磁场中运动，洛伦兹力作向心力可得，解得①；

当θ=0°时，如图所示，可知粒子打在PQ上的位置为O点水平线上方处；

当θ增大时，粒子打在PQ上的位置下移，知道粒子的运动轨迹与PQ相切时，如图所示，可知粒子打在PQ上的位置为O点水平线下方处；

当θ继续增大直到180°，粒子的运动轨迹与PQ不相交，直接从MN上射出，且在MN上的出射点不断上移直到O点，所以，若只改变粒子速度方向，使θ角能在0°至180°间不断变化，则PQ边界上有粒子射出的区间长度为；若只改变粒子速度方向，使θ角能在0°至180°间不断变化，则粒子运动半径不变，那么粒子运动周期不变，所以，粒子在磁场中运动的轨迹所对应的弦长越长，则粒子在磁场中运动的越长，由D的分析可知，当粒子的出射点在PQ上时，粒子的弦长可取[a，2a]的任意值；当粒子的出射点在MN上时，粒子的弦长可取的任意值；所以，粒子运动轨迹的弦长最大可取，此时对应的中心角φ=120°，所以联立①式子可知，粒子在磁场中运动的最长时间，故C正确．

练习册系列答案

A. 4s末物体的速度为m/s

B. 最初4 s内物体的位移为m

C. 从开始至6 s末物体都做曲线运动

D. 最初4 s内物体做直线运动，接下来的2 s内物体做曲线运动

【题目】为了测定一段由均匀材料制成的圆柱体的电阻率(电阻在200～250 Ω之间)，现给定电压表V(量程6 V、内阻约为5 kΩ)、电流表A(量程30 mA、内阻约为40 Ω)、滑动变阻器R(0～15 Ω)、电源(E＝6 V)、开关S及导线若干.

(1)设计测量圆柱体电阻Rx的电路图，并画在虚线框内___________；

(2)如图所示中的6个点分别表示实验中测得的6组电压表U和电流表I的值，试根据图求出圆柱体电阻Rx＝________ Ω(结果保留2位有效数字)；

(3)用50分度的游标卡尺测得该圆柱体的长度l如图甲所示，则l＝________ mm；用螺旋测微计测圆柱体的直径d如图乙所示，则d＝________ mm.

(4)由以上数据求出ρ＝___________ Ω·m(保留两位有效数字).

【题目】为了测量两个质量不等的沙袋的质量，由于没有直接测量工具，某实验小组应用下列器材测量：轻质定滑轮(质量和摩擦可忽略)、砝码一套(总质量为m＝0.5 kg)、细线、米尺、秒表，他们根据已学过的物理学知识，改变实验条件进行多次测量，选择合适的变量得到线性关系，作出图线并根据图线的斜率和截距求出沙袋的质量．操作如下：g=10m/s2

(1)实验装置如图，设左右两边沙袋的质量分别为m1、m2；

(2)从m中取出质量为m′的砝码放在右边沙袋中，剩余砝码都放在左边沙袋中，发现m1下降m2上升；

(3)用米尺测出沙袋m1从静止下降的距离h，用秒表测出沙袋m1下降时间t，则可知沙袋的加速度大小为a＝________

(4)改变m′，测量相应的加速度a，得到多组m′及a的数据，作出________(选填“a～m′” 或“a～1/m′”)图线；

(5)若求得图线的斜率k＝4 m/kg·s2，截距b＝2 m/s2，沙袋的质量m1＝________kg，m2＝________kg。

【题目】在探究加速度与力、质量的关系实验中，采用如图1所示的实验装置，小车及车中砝码的质量用M表示，盘及盘中砝码的质量用m表示，小车的加速度可由小车后拖动的纸带打上的点计算出．

（1）当M与m的大小关系满足时，才可以认为绳对小车的拉力大小等于盘及盘中砝码的重力．

（2）一组同学在做加速度与质量的关系实验时，保持盘及盘中砝码的质量一定，改变小车及车中砝码的质量，测出相应的加速度，采用图象法处理数据．为了比较容易地观测加速度a与质量M的关系，应该做a与的图象．

（3）某组同学实验得出数据，画出a﹣F图象如图2所示，那么该组同学实验中出现的问题可能是

A．实验中摩擦力没有平衡

B．实验中摩擦力平衡过度

C．实验中绳子拉力方向没有跟平板平行

D．实验中小车质量发生变化

【题目】如图所示，不同带电粒子以不同速度由左端中线水平射入如图装置，左侧有竖直向下的匀强电场E和垂直于纸面向内的匀强磁场B1，右侧是垂直于纸面向外的磁场B2，中间有一小孔，不计粒子重力。下列说法正确的是

A. 只有正电荷才能沿中线水平通过B1区域进入到B2磁场区域。

B. 只有速度的粒子才能沿中线水平通过B1区域进入到B2磁场区域

C. 如果粒子打在胶片上离小孔的距离是d，则该粒子的荷质比为

D. 若甲、乙两个粒子的电荷量相等，打在胶片上离小孔的距离是2：3，则甲、乙粒子的质量比为2：3

【题目】如图所示，一个绝缘且内壁光滑的环形细圆管，固定于竖直平面内，环的半径为R（比细管的内径大得多），在圆管内的最低点有一个直径略小于细管内径的带正电小球处于静止状态，小球的质量为m，带电荷量为q，重力加速度为g．空间存在一磁感应强度大小未知（不为零），方向垂直于球形细圆管所在平面且向里的匀强磁场．某时刻，给小球一方向水平向右，大小为的初速度，则以下判断正确的是（）