题目内容
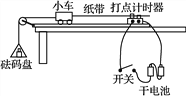
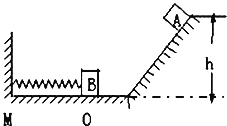
【题目】如图所示，一个半径为R=2.0m的水平圆盘绕过圆心的竖直轴转动，转动角速度为ω=5.0rad/s。在A处有一个小滑块随圆盘一起转动，某一时刻，滑块从圆盘边缘滑落，经光滑的过渡圆管进入光滑斜面轨道AB。已知AB段斜面倾角为37°。滑块在运动过程中始终未脱离轨道，不计在过渡圆管处的机械能损失。(g=10m/s2，sin37°=0.6。cos37°=0.8，结果保留两位有效数字)
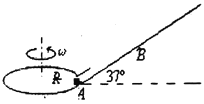
(1)若AB间的距离为3.0m，求滑块从A运动至B点的时间：
(2)滑块从开始上滑、到再下滑回A处的过程中，圆盘转动的圈数。
【答案】（1）t1 =0.33s，t2=3.0s （2）2.7
【解析】（1）滑块做圆周运动，有v0=ωR=10m/s
滑块向上运动时加速度a，由牛顿第二定律得mgsin37°=ma
运动至B点时，由运动规律得s＝v0t+
at2
联立上述各式并代入数据得: t1=0.33s，t2=3.0s
（2）滑块返回A点的时间为t′，由运动规律得
由运动规律得圆盘转动周期为
t2时间圆盘转动的圈数为n＝
联立各式、代入数据得n=2.7
练习册系列答案
阅读快车系列答案
相关题目
