Question

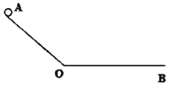
【题目】如图所示，质量为km小球a，用l1=0.4m的细线悬挂于O1点，质量为m小球b，用l2=0.8m的细线悬挂于O2点，且O1、O2两点在同一条竖直线上。让小球a静止下垂，将小球b向右拉起，使细线水平，从静止释放，两球刚好在最低点对心相碰。相碰后，小球a向左摆动，细线与竖直方向最大偏角为600，两小球可视为质点，空气阻力忽略不计，仅考虑首次碰撞。取g=10m/s2。

求：（1）两球相碰前小球b的速度大小；

（2）讨论k可能的取值范围

（3）所有满足题干要求的碰撞情形中，k取何值时？机械能损失最多。

Answer 1

【答案】（1）4m/s（2）（3）时，动能损失最大

【解析】（1）对小球b下摆过程： ，得出碰前，

（2）小球a上摆过程： ，碰后

对两球碰撞过程有，得出。

由碰撞过程动能不增加有： ，得出，

此外由碰撞中合理性原则不可穿得： ，得出。

综上所述

（3）碰撞中动能损失

可以得出当时，动能损失最大。