题目内容
6.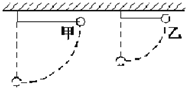 甲、乙两球质量相同,悬线一长一短,如将两球从如图所示位置,由同一水平面无初速释放,不计阻力,则小球通过最低点的时刻:
甲、乙两球质量相同,悬线一长一短,如将两球从如图所示位置,由同一水平面无初速释放,不计阻力,则小球通过最低点的时刻:①两球受到的拉力大小相等
②两球的动量相同
③两球的向心加速度相同
④相对同一参考平面,两球机械能相等
以上说法正确的是( )
| A. | 只有②③④ | B. | 只有①③④ | C. | 只有②④ | D. | 只有②③ |
分析 根据动能定理即可求解A答案,根据圆周运动向心力公式及动能定理即可求得B答案,根据向心力公式即可求解C答案,由重力做功多少,重力势能就减少多少,分析D项.
解答 解:①从同一水平面无初速释放到小球通过最低点的过程中运用动能定理可知:小球的末动能等于小球重力所做的功,由动能定理得:
mgl=$\frac{1}{2}m{v}^{2}$
所以:v=$\sqrt{2gl}$在最低点有:F-mg=m$\frac{{v}^{2}}{l}$,解得:F=3mg,与绳长无关,故①正确;
②根据动量的定义式:P=mv,两球的速度不相等,所以 动量不相同.故②错误;
③通过最低点时,两球的向心加速度为:a=$\frac{{v}^{2}}{l}$=2g,与绳长无关,故③正确;
④相对同一参考平面,两球开始时的重力势能相等;因机械能守恒;则两球机械能相等;故④正确;
故选:B.
点评 本题主要考查了动能定理、圆周运动向心力公式及向心加速度公式、机械能守恒定律得应用;要注意根据机械能守恒定律推导BC两项,并可以作为结论应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.一辆汽车在水平地面上转弯时,地面的摩擦力已达到最大,当这辆汽车速率增为原来的2倍时,则为避免发生事故,它在同样地面转弯的轨道半径应该( )
| A. | 减为原来的$\frac{1}{2}$ | B. | 减为原来的$\frac{1}{4}$ | C. | 增为原来的2倍 | D. | 增为原来的4倍 |
17.2010年10月1日18时59分57秒,随着嫦娥二号在西昌卫星发射中心成功升空,中国探月工程二期揭开序幕.在经历了星箭分离、卫星入轨、中途修正、约111小时近35万公里的行程后,北京时间6日11时6分,在北京航天飞行控制中心的精确控制下,嫦娥二号卫星成功实施第一次近月制动,32分钟后,卫星顺利进入周期约12小时的椭圆环月轨道,为嫦娥二号最终进入“使命轨道”进行科学探测活动奠定了坚实基础.联系所学的物理知识,进行的下列推断正确的是( )
| A. | 在点火阶段,由于平均加速度很难超过重力加速度,所以该阶段为失重阶段 | |
| B. | 嫦娥二号卫星实施近月制动后,速度会减小,动能转化为势能,卫星会靠近月球 | |
| C. | 若已知嫦娥二号的轨道半径和周期,就可以算出卫星的质量 | |
| D. | 嫦娥二号卫星的质量减小,则飞船速率会减小 |
14.有下列几种情景,请根据所学知识选择对情景的分析和判断正确的说法( )
| A. | 点火后即将升空的火箭,因火箭还没运动,所以加速度一定为零 | |
| B. | 太空中的“天宫一号”绕地球匀速转动,其加速度为零 | |
| C. | 高速行驶的磁悬浮列车,因速度很大,所以加速度也一定很大 | |
| D. | 高速公路上沿直线高速行驶的轿车为避免事故紧急刹车.因轿车紧急刹车,速度变化很快,所以加速度很大 |
11.一质量为1Kg的物体从静止开始向下做匀加速直线运动,经3s落地,落地时的速度大小为10m/s,取g=10m/s2,则下列判断正确的是( )
| A. | 物体的机械能减少了100J | B. | 物体的重力势能减少了50J | ||
| C. | 重力对物体做功为150J | D. | 物体克服阻力做功50J |
18.下列说法中正确的有( )
| A. | 只要闭合电路内有磁通量,闭合电路中就有感应电流产生 | |
| B. | 穿过闭合线圈的磁通量发生变化时,闭合线圈就一定有感应电流产生 | |
| C. | 线框不闭合时,若穿过线圈的磁通量发生变化,线圈中没有感应电流和感应电动势 | |
| D. | 线框不闭合时,若穿过线圈的磁通量发生变化,线圈中没有感应电流,但有感应电动势 |
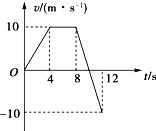 如图所示,是某质点运动的v-t图象,请回答:
如图所示,是某质点运动的v-t图象,请回答: 如图所示,A、B两物体位于光滑水平面上,仅限于沿同一直线运动.当它们之间的距离大于等于某一定值d时,相互作用力为零;当它们之间的距离小于d时,存在大小恒为F的斥力.设A物体质量m1=1.0kg,开始时静止在直线上某点;B物体质量m2=3.0kg,以速度v0从远处沿该直线向A运动.若d=0.10m,F=0.60N,v0=0.20m/s,求:
如图所示,A、B两物体位于光滑水平面上,仅限于沿同一直线运动.当它们之间的距离大于等于某一定值d时,相互作用力为零;当它们之间的距离小于d时,存在大小恒为F的斥力.设A物体质量m1=1.0kg,开始时静止在直线上某点;B物体质量m2=3.0kg,以速度v0从远处沿该直线向A运动.若d=0.10m,F=0.60N,v0=0.20m/s,求: