题目内容
如图所示，在场强为E的竖直向下匀强电场中有一块水平放置的足够大的接地金属板，在金属板的正上方高为h处有一个小的放射源，放射源上方有一铅板，使放射源可以向水平及斜下方各个方向释放质量为m、电量为q、初速度为v0的带电粒子，粒子最后落在金属板上，不计粒子重力．试求：
（1）粒子打在板上时的动能；
（2）计算落在金属板上的粒子图形的面积大小．
（1）
（2）
解析试题分析：（1）电场力做功与路径无关，只与始末位置间的电势差有关，所以粒子在下落过程中电场力做的功为
粒子在整个过程中仅有电场力做功，由动能定理得：
解得：粒子打在板上时的动能为
（2）因不计粒子重力，粒子在电场中仅受电场力作用，水平射出后将做类平抛运动，粒子下降过程沿电场方向做初速度为零的匀加速直线运动，水平方向做匀速直线运动．由牛顿第二定律知：
所以粒子下降过程加速度为：
设粒子下降过程沿电场方向做匀变速运动的时间为t，则：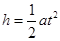
解得：
粒子水平射出后将做类平抛运动，此粒子沿水平方向的位移大小即是落在金属板上的粒子圆形面积的半径，设水平位移为x，则根据运动学公式有：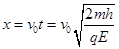
由几何知识知圆形面积为：
考点：本题考查带电粒子在匀强电场中的运动、牛顿第二定律及动能定理的应用，意在考查考生处理类平抛运动问题的能力．
练习册系列答案
相关题目
，电子的重力忽略不计，求：
范围内，要求带电粒子仍能通过Q点，求此电场左边界的横坐标x′与电场强度的大小E′的函数关系。
