Question

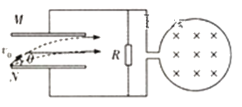
【题目】如图所示，一面积为S的n匝圆形金属线圈与阻值为R的电阻连接成闭合回路，金属线圈的电阻也为R，导线的电阻不计。线圈内存在一个方向垂直纸面向里、磁感应强度随时间均匀增加且变化率为k的磁场。电阻两端并联一对水平放置的平行金属板，金属板长为L、极板间距为，极板间电场均匀分布。现有一粒子以大小为的初速度从下极板左边缘飞入板间，粒子恰好从上极板右边缘水平飞出，粒子重力不计，求：

(1)粒子的带电性质及与水平极板间的夹角θ；

(2)若保持大小不变但改变的方向，使得带电粒子恰能沿极板中央轴线水平飞出，则需要把磁感应强度的变化率调整为原来的多少倍。

Answer 1

【答案】(1)；(2)

【解析】

(1)根据楞次定律可知线圈的电流为逆时针，则上极板带正电，带电粒子在竖直方向做匀减速，因此由带电粒子在电场中运动的轨迹可判断出粒子带正电，把粒子的运动分解为水平方向的匀速直线运动和竖直方向的匀减速直线运动，则有

联立解得

(2)设此时初速度方向与水平极板间的夹角为，

粒子在极板间做类平抛运动的逆运动，有

联立解得

，

极板两端的电压

感应电动势

则

，

因为

联立解得

。