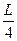题目内容
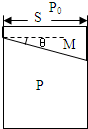
如图所示,导热汽缸固定在水平地面上,用质量为M的光滑的活塞Q封闭了一定质量热力学温度为T1的理想气体.一不可伸长的细绳绕过定滑轮,一端拴住活塞,另一端栓着质量为m的重物.已知大气压强为p0,活塞的位置离底部距离为H,活塞的截面积为S.最初整个系统处于静止状态,(滑轮质量、滑轮轴上的摩擦和空气阻力均不计).求:
(1)剪断细绳当系统再次稳定时,活塞的位置离底部的距离h;
(2)再次稳定后,对汽缸加热,使活塞再次回到最初的位置,此时气体的温度T2.

(1)剪断细绳当系统再次稳定时,活塞的位置离底部的距离h;
(2)再次稳定后,对汽缸加热,使活塞再次回到最初的位置,此时气体的温度T2.

(1)初态稳定时活塞处于平衡状态由受力平衡得:mg+p1S=p0S+Mg
得:p1=p0+
剪断再次稳定后活塞处于平衡状态由受力平衡得:p2=p0+
从第一个稳定状态到第二个稳定状态经历了等温过程由玻意耳定律:p1V1=p2V2
可得:[P0+
]?(HS)=(P0+
)?(hS)
计算得:h=
(2)从第一个稳定状态到第三个稳定状态经历了等容过程由查理定律:
=
且P2=p3
可得:
=
计算得:T2=
答:(1)剪断细绳当系统再次稳定时,活塞的位置离底部的距离h为
;
(2)再次稳定后,对汽缸加热,使活塞再次回到最初的位置,此时气体的温度为
.
得:p1=p0+
| (M-m)g |
| S |
剪断再次稳定后活塞处于平衡状态由受力平衡得:p2=p0+
| Mg |
| S |
从第一个稳定状态到第二个稳定状态经历了等温过程由玻意耳定律:p1V1=p2V2
可得:[P0+
| (M-m)g |
| S |
| Mg |
| S |
计算得:h=
| (p0S+Mg-mg)H |
| p0S+Mg |
(2)从第一个稳定状态到第三个稳定状态经历了等容过程由查理定律:
| P1 |
| T1 |
| P3 |
| T3 |
可得:
P0+
| ||
| T1 |
P0+
| ||
| T2 |
计算得:T2=
| (P0S+Mg)T1 |
| P0S+(M-m)g |
答:(1)剪断细绳当系统再次稳定时,活塞的位置离底部的距离h为
| (p0S+Mg-mg)H |
| p0S+Mg |
(2)再次稳定后,对汽缸加热,使活塞再次回到最初的位置,此时气体的温度为
| (P0S+Mg)T1 |
| P0S+(M-m)g |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目