题目内容
(2006?上海)辨析题:要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.
某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度 v1=40m/s,然后再减速到v2=20m/s,
t1=
=…; t2=
=…; t=t1+t2
你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
| 启动加速度a1 | 4m/s2 |
| 制动加速度a2 | 8m/s2 |
| 直道最大速度v1 | 40m/s |
| 弯道最大速度v2 | 20m/s |
| 直道长度s | 218m |
t1=
| v1 |
| a1 |
| v1-v2 |
| a2 |
你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
分析:直道的长度是一定的,当达到最大速度之后再减速的总的位移的大小要大于直道的长度,即摩托车不能达到最大的速度,否则达到弯道时就要偏出车道;
最短的时间应该是摩托车以最大的加速度加速之后接着以最大的加速度减速运动,达到弯道时的速度恰好为弯道最大速度v2,根据加速和减速的位移的关系可以求得时间的大小.
最短的时间应该是摩托车以最大的加速度加速之后接着以最大的加速度减速运动,达到弯道时的速度恰好为弯道最大速度v2,根据加速和减速的位移的关系可以求得时间的大小.
解答:解:不合理.
因为按这位同学的解法可得
t1=
=10s,
t2=
=2.5s,
所以加速距离
s1=
t1=200m,
s2=
t2=75m,
总位移s1+s2=275m>s.故不合理.
由上可知摩托车不能达到最大速度v2,设满足条件的最大速度为v,
则:
+
=s
解得:v=36m/s
又加速的时间为 t1=
=9s
减速的时间为 t2=
=2 s
因此所用的最短时间 t=t1+t2=11s.
因为按这位同学的解法可得
t1=
| v1 |
| a1 |
t2=
| v1-v2 |
| a2 |
所以加速距离
s1=
| v1 |
| 2 |
s2=
| v1+v2 |
| 2 |
总位移s1+s2=275m>s.故不合理.
由上可知摩托车不能达到最大速度v2,设满足条件的最大速度为v,
则:
| v2 |
| 2a1 |
v2-
| ||
| 2a2 |
解得:v=36m/s
又加速的时间为 t1=
| v |
| a1 |
减速的时间为 t2=
| v-v2 |
| a2 |
因此所用的最短时间 t=t1+t2=11s.
点评:摩托车先加速接着再减速,由位移的关系可以求得结果,解本题的关键是分析清楚摩托车的运动的过程.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 (2006?上海模拟)如图所示(a),一条长为3L的绝缘丝线穿过两个质量都是m的小金属环A和B,将丝线的两端共同系于天花板上的O点,使金属环带电后,便因排斥而使丝线构成一个等边三角形,此时两环恰处于同一水平线上,若不计环与线间的摩擦,求金属环所带电量是多少?某同学在解答这道题时的过程如下:
(2006?上海模拟)如图所示(a),一条长为3L的绝缘丝线穿过两个质量都是m的小金属环A和B,将丝线的两端共同系于天花板上的O点,使金属环带电后,便因排斥而使丝线构成一个等边三角形,此时两环恰处于同一水平线上,若不计环与线间的摩擦,求金属环所带电量是多少?某同学在解答这道题时的过程如下: (2006?上海模拟)(A类题)一圆柱形气缸,质量M为10kg,总长度L为40cm,内有一厚度不计的活塞,质量m为5kg,截面积S为50cm2,活塞与气缸壁间摩擦不计,但不漏气,当外界大气压强p0为1×105 Pa,温度t0为7℃时,如果用绳子系住活塞将气缸悬挂起来,如图所示,气缸内气体柱的高L1为35cm,(g取10m/s2)求:
(2006?上海模拟)(A类题)一圆柱形气缸,质量M为10kg,总长度L为40cm,内有一厚度不计的活塞,质量m为5kg,截面积S为50cm2,活塞与气缸壁间摩擦不计,但不漏气,当外界大气压强p0为1×105 Pa,温度t0为7℃时,如果用绳子系住活塞将气缸悬挂起来,如图所示,气缸内气体柱的高L1为35cm,(g取10m/s2)求: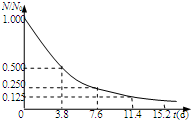 (2006?上海模拟)(A类题)如图,纵坐标表示某放射性物质中未衰变的原子核数(N)与原来总原子核数(N0)的比值,横坐标表示衰变的时间,则由图线可知该放射性物质的半衰期为
(2006?上海模拟)(A类题)如图,纵坐标表示某放射性物质中未衰变的原子核数(N)与原来总原子核数(N0)的比值,横坐标表示衰变的时间,则由图线可知该放射性物质的半衰期为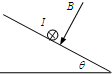 (2006?上海模拟)(A类题)在倾角为θ的光滑供销斜面上垂直纸面放一根长为L,质量为m的直导体棒,一匀强磁场垂直于斜面向下,如图所示,当导体棒内通有垂直纸面向里的电流I时,导体棒恰好静止在斜面上,则磁感应强度的大小为
(2006?上海模拟)(A类题)在倾角为θ的光滑供销斜面上垂直纸面放一根长为L,质量为m的直导体棒,一匀强磁场垂直于斜面向下,如图所示,当导体棒内通有垂直纸面向里的电流I时,导体棒恰好静止在斜面上,则磁感应强度的大小为