题目内容
5. (1)如图所示,两平行金属板A、B板间电压恒为U,一束波长为的入射光射到金属板B上,使B板发生了光电效应,已知该金属板的逸出功为W,电子的质量为m.电荷量为e,已知普朗克常量为h,真空中光速为c,下列说法中正确的是ABD
(1)如图所示,两平行金属板A、B板间电压恒为U,一束波长为的入射光射到金属板B上,使B板发生了光电效应,已知该金属板的逸出功为W,电子的质量为m.电荷量为e,已知普朗克常量为h,真空中光速为c,下列说法中正确的是ABDA.入射光子的能量为h$\frac{c}{λ}$
B.到谜A板的光电子的最大动能为h$\frac{c}{λ}$-W+eU
C.若增大两板间电压B板没有光电子逸出
D.若减小入射光的波长一定会有光电子逸出
E.若增大入射光的频率金属板的逸出功将大于w.
分析 A、根据E=hv,而v=$\frac{c}{λ}$,即可求解;
B、根据光电效应方程Ekm=h$\frac{c}{λ}$-W,再结合动能定理,则有求得到达A板的动能;
C、极板间电压与是否有光电子逸出无关;
D、根据光电效应发生条件,结合波长与频率关系,即可求解;
E、金属板的逸出功W=hv0,与入射光的频率无关.
解答 解:A、根据E=hv,而v=$\frac{c}{λ}$,则光子的能量为h$\frac{c}{λ}$,故A正确;
B、光电子的逸出最大动能Ekm=h$\frac{c}{λ}$-W,根据动能定理,Ekm′-Ekm=eU,则当到达A板的光电子的最大动能为h$\frac{c}{λ}$-W+eU,故B正确;
C、若增大两板间电压时,不会影响光电效应现象,仍有光电子逸出,故C错误;
D、若减小入射光的波长,那么频率增大,仍一定会有光电子逸出,故D正确;
E、金属板的逸出功与极限频率有关,与入射率无关,故E错误;
故选:ABD.
点评 解决本题的关键掌握发生光电效应的条件是入射光的频率大于截止频率.以及知道动能定理的应用,并理解光电效应方程的应用,注意入射光的频率决定光电子的最大初动能.

练习册系列答案
相关题目
12.一物体受到两个力F1和F2,它们之间的夹角为θ,则( )
| A. | 若θ为锐角,保持F1不变而使F2减小,则合力减小 | |
| B. | 若θ为钝角,保持F1不变而使F2减小,则合力减小 | |
| C. | 若θ为钝角,保持F1不变而使F2减小,则合力增大 | |
| D. | 若保持F1和F2不变而使θ减小,则合力一定增大 |
17. 如图所示一升降机在箱底装有若干个可视为轻质的弹簧,设在某次事故中,升降机吊索在空中断裂,忽略一切摩擦及阻力,则下降的升降机在从弹簧下端刚好触地直到升降机运动至最低点的过程中,下列说法中正确的是( )
如图所示一升降机在箱底装有若干个可视为轻质的弹簧,设在某次事故中,升降机吊索在空中断裂,忽略一切摩擦及阻力,则下降的升降机在从弹簧下端刚好触地直到升降机运动至最低点的过程中,下列说法中正确的是( )
 如图所示一升降机在箱底装有若干个可视为轻质的弹簧,设在某次事故中,升降机吊索在空中断裂,忽略一切摩擦及阻力,则下降的升降机在从弹簧下端刚好触地直到升降机运动至最低点的过程中,下列说法中正确的是( )
如图所示一升降机在箱底装有若干个可视为轻质的弹簧,设在某次事故中,升降机吊索在空中断裂,忽略一切摩擦及阻力,则下降的升降机在从弹簧下端刚好触地直到升降机运动至最低点的过程中,下列说法中正确的是( )| A. | 升降机的速度不断减小 | |
| B. | 升降机的加速度不断变大 | |
| C. | 先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功 | |
| D. | 到最低点时,升降机加速度的值等于重力加速度的值 |

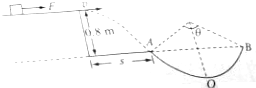 一质量m=2kg的物体,由静止开始,在水平拉力F的作用下在距地面高度h=0.8m的光滑平台上运动,一段时间后,撤去力F,物体继续运动到达平台右端后离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,平台右端到A点的水平距离s=1.2m,取g=10m/s2,求:
一质量m=2kg的物体,由静止开始,在水平拉力F的作用下在距地面高度h=0.8m的光滑平台上运动,一段时间后,撤去力F,物体继续运动到达平台右端后离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,平台右端到A点的水平距离s=1.2m,取g=10m/s2,求: 水平面上固定着直角支架ABC,支架所在平面与水平面垂直,在AC和BC杆上分别套有质量为m1和m2的光滑圆环,且m1和m2用轻质细线相连,如图所示,已知AC与水平面的夹角为θ,求m1和m2平衡后,细线上的拉力.
水平面上固定着直角支架ABC,支架所在平面与水平面垂直,在AC和BC杆上分别套有质量为m1和m2的光滑圆环,且m1和m2用轻质细线相连,如图所示,已知AC与水平面的夹角为θ,求m1和m2平衡后,细线上的拉力.