题目内容
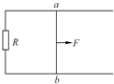
【题目】如图所示,两根平行金属导轨固定在水平桌面上,每根导轨每米的电阻为r0=0.10Ω/m,导轨的端点P、Q用电阻可以忽略的导线相连,两导轨间的距离l=0.20m。有随时间变化的匀强磁场垂直于桌面,已知磁感应强度B与时间t的关系为B=kt,比例系数k=0.020T/s。一电阻不计的金属杆可在导轨上无摩擦低滑动,在滑动过程中保持与导轨垂直。在t=0时刻,金属杆紧靠在P、Q端,在外力作用下,杆以恒定的加速度从静止开始向导轨的另一端滑动,求在t=6.0s时金属杆所受的安培力。
![]()
【答案】1.44×10-3N
【解析】
以a表示金属杆运动的加速度,在t时刻,金属杆与初始位置的距离L=![]() at2,此时杆的速度v=at,杆与导轨构成的回路的面积S=Ll,回路中的感应电动势E=S
at2,此时杆的速度v=at,杆与导轨构成的回路的面积S=Ll,回路中的感应电动势E=S![]() +Blv,而B=kt,故
+Blv,而B=kt,故
![]() =
=![]() =k
=k
回路的总电阻R=2Lr0;回路中的感应电流I=![]() ;
;
作用于杆的安培力F=BlI.
联立以上各式解得F=![]() ·
·![]() t.
t.
代入数据得F=1.44×10-3N.
点评 当问题中同时有动生电动势和感生电动势时,可以分别单独求出动生电动势和感生电动势,再结合其方向求出电路中的总电动势.若两电动势方向相同,直接相加;若两电动势方向相反,用大电动势减去小电动势,总电动势方向与大的方向一致.在单独求出动生电动势时,磁感应强度B应该运用该时刻的值运算;单独求感生电动势时,面积S应该运用此时的面积运算.该方法也是分解思想的体现.当然,如果运用公式E=n![]() 计算,求得的电动势也为总电动势.解题时是运用分解的方法分别求出两个电动势后再合成,还是直接用E=n
计算,求得的电动势也为总电动势.解题时是运用分解的方法分别求出两个电动势后再合成,还是直接用E=n![]() 计算,由题中条件决定.
计算,由题中条件决定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目