题目内容
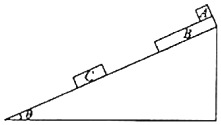
【题目】如图所示,固定在水平面上的斜面体倾角为θ=37°,斜面足够长。长为L、质量为m的长木板B放在斜面顶端,长为![]() L、质量为
L、质量为![]() m的木板C也放在斜面上,B、C均处于锁定状态。木板B与斜面间的动摩擦因数为μ2=0.5,B、C两木板厚度相同,两板间距离为L.将质量为
m的木板C也放在斜面上,B、C均处于锁定状态。木板B与斜面间的动摩擦因数为μ2=0.5,B、C两木板厚度相同,两板间距离为L.将质量为![]() m的物块A(可视为质点)轻放在长木板B的顶端,同时解除木板B的锁定,A、B均从静止开始做匀加速直线运动。当木板B与C刚好要相碰时,解除木板C的锁定,此时物块A刚好要滑离木板B,已知木板B与C相碰后粘在一起(碰撞时间极短),重力加速度为g,sin37°=0.6,求:
m的物块A(可视为质点)轻放在长木板B的顶端,同时解除木板B的锁定,A、B均从静止开始做匀加速直线运动。当木板B与C刚好要相碰时,解除木板C的锁定,此时物块A刚好要滑离木板B,已知木板B与C相碰后粘在一起(碰撞时间极短),重力加速度为g,sin37°=0.6,求:
(1)物块A与B间的动摩擦因数μ1
(2)从开始运动到B与C刚好要相碰,系统因摩擦产生的热量Q;
(3)若B、C碰撞后,BC整体和A都恰好做匀速运动,求A在C上滑行的时间。
【答案】(1)物块A与B间的动摩擦因数为![]() ;(2)从开始运动到B与C刚好要相碰,系统因摩擦产生的热量Q为
;(2)从开始运动到B与C刚好要相碰,系统因摩擦产生的热量Q为![]() mgL;(3)A在C上滑行的时间为
mgL;(3)A在C上滑行的时间为![]()
【解析】
(1)设A和B匀加速时的加速度大小分别为a1和a2,B碰C前运动的时间为t1
对A和B分别用牛顿第二定律有:
![]() mgsinθ-μ1×
mgsinθ-μ1×![]() mgcosθ=
mgcosθ=![]() ma1
ma1
mgsinθ+μ1×![]() mgcosθ-μ2(m+
mgcosθ-μ2(m+![]() m)gcosθ=ma2
m)gcosθ=ma2
2L=![]() a1
a1![]()
L=![]()
求得![]()
(2)A在B上滑动时因摩擦产生的热量为
Q1=μ1×![]() mgcosθL
mgcosθL
从开始运动到B与C刚好要相碰时的一段时间内,B与斜面间的摩擦产生的热量
Q2=μ2×![]() mgcosθL
mgcosθL
此时整个系统因摩擦产生的热量Q=Q1+Q2
联立解得:Q=![]() mgL
mgL
(3)由(1)问求得物块A滑动的加速度大小为a1=![]()
木板B运动的加速度大小为a2=![]() g
g
当B和C刚要相碰时,A,B运动的时间t1=![]()
当B和C相碰前一瞬间,A的速度大小v1=a1t1=![]()
B的速度大小v2=a2t1=![]()
B与C碰撞的过程动量守恒。设碰撞粘在一起的一瞬间,B,C的共同速度为v3,
根据动量守恒定律有mv2=(m+![]() m)v3
m)v3
求得v3=![]()
由题意碰后,A和BC都做匀速运动
设物块A在板C上滑行的时间为t2,则t2=![]() =
=![]()