题目内容
如图所示,一根竖直杆穿过一个质量M=2.0kg的带孔的物块A,另一正方形金属线框B的质量m=2.7kg、边长a=0.16m.杆的右侧距杆L=2.0m处固定有一定滑轮,一柔软绝缘的细绳跨过定滑轮,两端分别与物块A和B连接.开始时滑轮左侧的绳子处在水平方向上,让A、B同时由静止释放,B向上运动h=0.5m便进入长度b=0.16m的指向纸内的磁感应强度B=0.5T的匀强磁场,经过磁场过程线框做匀速运动;而后A沿竖直杆下滑.不计一切摩擦和空气阻力,g取10m/s2,sin37°=0.6,cos37°=0.8, ≈1.41.
≈1.41.(1)求线框B上边刚进入磁场时的速度;
(2)问线框B经过磁场过程中物块A向下做什么运动?
(3)求线框B经过匀强磁场时获得的内能.

【答案】分析:(1)将A的速度进行分解,A在沿绳子方向上的速度等于B的速度,在B未进入磁场时,抓住系统机械能守恒定律求出B上边刚进入磁场时的速度.
(2)根据A与B的速度关系,B的速度大小不变,抓住夹角的变化判断出A的运动的情况.
(3)分别求出B进入磁场时和出磁场时A的速度,然后对系统研究,运用能量守恒定律求出线框B经过匀强磁场时获得的内能.
解答:解:(1)设B上升了h时绳子与水平方向的夹角为θ
cosθ= =0.8…①
=0.8…①
此时A、B的速度大小关系为vA= …②
…②
A下降的高度为H1=Ltgθ=1.5m…③
A下降B上升过程中,A、B组成系统机械能守恒:MgH1=mgh+ MvA2+
MvA2+ mvB2…④
mvB2…④
将①②③代入④可得线框B上边刚进入磁场时的 速度vB≈2.0m/s.
(2)根据vA= ,当线框B匀速通过磁场的过程中,随着θ的增大,物块A做变减速运动.
,当线框B匀速通过磁场的过程中,随着θ的增大,物块A做变减速运动.
(3)当线框B下边刚离开磁场时,设绳子与水平方向的夹角为θ′,
cosθ′= ≈
≈ …⑤
…⑤
此时A、B的速度大小关系为vA′= =2
=2 m/s…⑥
m/s…⑥
设从B开始上升起,A下降高度为H2,则H2=Ltgθ′=2.0m…⑦
设线框B经过匀强磁场时获得的内能Q,整个过程中,A、B组成的系统能量守恒,有:
MgH2=mg(h+a+b)+ MvA′2+
MvA′2+ mvB2+Q…⑧
mvB2+Q…⑧
联立⑤⑥⑦⑧并代入vB≈2.0m/s的值,可求得:Q=4.46J
答:(1)线框B上边刚进入磁场时的速度为2.0m/s.
(2)线框B经过磁场过程中物块A向下做变减速运动.
(3)线框B经过匀强磁场时获得的内能为4.46J.
点评:本题综合考查了系统机械能守恒、能量守恒,综合性较强,对学生能力要求较高,需加强训练.
(2)根据A与B的速度关系,B的速度大小不变,抓住夹角的变化判断出A的运动的情况.
(3)分别求出B进入磁场时和出磁场时A的速度,然后对系统研究,运用能量守恒定律求出线框B经过匀强磁场时获得的内能.
解答:解:(1)设B上升了h时绳子与水平方向的夹角为θ
cosθ=
 =0.8…①
=0.8…①此时A、B的速度大小关系为vA=
 …②
…②A下降的高度为H1=Ltgθ=1.5m…③
A下降B上升过程中,A、B组成系统机械能守恒:MgH1=mgh+
 MvA2+
MvA2+ mvB2…④
mvB2…④将①②③代入④可得线框B上边刚进入磁场时的 速度vB≈2.0m/s.
(2)根据vA=
 ,当线框B匀速通过磁场的过程中,随着θ的增大,物块A做变减速运动.
,当线框B匀速通过磁场的过程中,随着θ的增大,物块A做变减速运动.(3)当线框B下边刚离开磁场时,设绳子与水平方向的夹角为θ′,
cosθ′=
 ≈
≈ …⑤
…⑤此时A、B的速度大小关系为vA′=
 =2
=2 m/s…⑥
m/s…⑥设从B开始上升起,A下降高度为H2,则H2=Ltgθ′=2.0m…⑦
设线框B经过匀强磁场时获得的内能Q,整个过程中,A、B组成的系统能量守恒,有:
MgH2=mg(h+a+b)+
 MvA′2+
MvA′2+ mvB2+Q…⑧
mvB2+Q…⑧联立⑤⑥⑦⑧并代入vB≈2.0m/s的值,可求得:Q=4.46J
答:(1)线框B上边刚进入磁场时的速度为2.0m/s.
(2)线框B经过磁场过程中物块A向下做变减速运动.
(3)线框B经过匀强磁场时获得的内能为4.46J.
点评:本题综合考查了系统机械能守恒、能量守恒,综合性较强,对学生能力要求较高,需加强训练.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
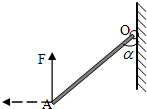 如图所示,一根均匀直杆OA可绕过O点且垂直于纸面的轴转动,在A端用竖直向上的力F将它拉到与竖直方向成α角的位置(α<90°),现将力F的方向沿逆时针方向缓慢转过90°,且在转动过程中,杆保持静止不动,力F和它的力矩M的变化情况是( )
如图所示,一根均匀直杆OA可绕过O点且垂直于纸面的轴转动,在A端用竖直向上的力F将它拉到与竖直方向成α角的位置(α<90°),现将力F的方向沿逆时针方向缓慢转过90°,且在转动过程中,杆保持静止不动,力F和它的力矩M的变化情况是( ) (2008?揭阳二模)如图所示,一根竖直杆穿过一个质量M=2.0kg的带孔的物块A,另一正方形金属线框B的质量m=2.7kg、边长a=0.16m.杆的右侧距杆L=2.0m处固定有一定滑轮,一柔软绝缘的细绳跨过定滑轮,两端分别与物块A和B连接.开始时滑轮左侧的绳子处在水平方向上,让A、B同时由静止释放,B向上运动h=0.5m便进入长度b=0.16m的指向纸内的磁感应强度B=0.5T的匀强磁场,经过磁场过程线框做匀速运动;而后A沿竖直杆下滑.不计一切摩擦和空气阻力,g取10m/s2,sin37°=0.6,cos37°=0.8,
(2008?揭阳二模)如图所示,一根竖直杆穿过一个质量M=2.0kg的带孔的物块A,另一正方形金属线框B的质量m=2.7kg、边长a=0.16m.杆的右侧距杆L=2.0m处固定有一定滑轮,一柔软绝缘的细绳跨过定滑轮,两端分别与物块A和B连接.开始时滑轮左侧的绳子处在水平方向上,让A、B同时由静止释放,B向上运动h=0.5m便进入长度b=0.16m的指向纸内的磁感应强度B=0.5T的匀强磁场,经过磁场过程线框做匀速运动;而后A沿竖直杆下滑.不计一切摩擦和空气阻力,g取10m/s2,sin37°=0.6,cos37°=0.8,
