题目内容
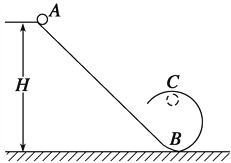
【题目】如图所示，斜槽轨道下端与一个半径为R=0.4 m的圆形轨道相连接．一个质量为0.1 kg的物体从高为H=2 m的A点由静止开始滑下，运动到圆形轨道的最高点C处时，对轨道的压力等于物体的重力．求物体从A运动到C的过程中克服摩擦力所做的功．(g取10 m/s2)
【答案】 0.8J
【解析】试题分析：小球到达C点时，小球竖直方向所受合力提供小球圆周运动向心力，从而求得小球在C点的速度，再根据动能定理求得小球从A到C过程中摩擦力做的功即可．
根据牛顿第三定律可知，小球在C点受到轨道的压力大小与重力相等
，方向竖直向下，又小球在C点时在竖直方向所受合力提供圆周运动向心力有： 
①
小球从A到C的过程中只有重力和摩擦力做功，根据动能定理有： 
②
联列①②两式代入
，可解得： 
因为摩擦力做负功所以克服摩擦力做0.8J的功．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
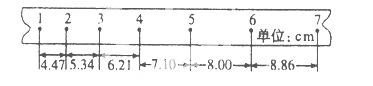
【题目】利用打点频率为50Hz打点计时器测定匀加速直线运动加速度，得到一条如图所示的纸带，按时间顺序取1、2、3、4、5、6、7个计数点，每相邻计数点间还有四个点未画出，测得相邻两个计数点间的距离如图所示，回答下列问题：
(1)接通打点计时器电源和让纸带开始运动，这两个操作之间的时间顺序关系是______
A．先接通电源，后让纸带运动 | B．先让纸带运动，再接通电源 |
C．让纸带运动的同时接通电源 | D．先让纸带运动或先接通电源都可以 |
(2)打点3时物体的速度为v3=______m/s（结果保留二位有效数字）
(3)由以上数据计算出物体运动的加速度为a=______m/s2（结果保留二位有效数字）
