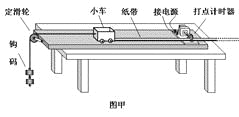
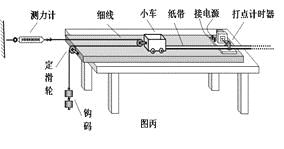
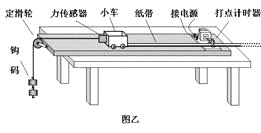
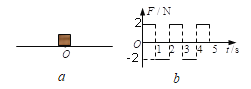题目内容
【题目】如图所示，一根质量不计的轻弹簧上端固定在天花板上，下端与一质量为m的托盘连接，托盘中有一个质量为2m的砝码．当托盘静止时，弹簧的伸长量为L．现将托盘向下拉，弹簧又伸长了L(未超过弹簧的弹性限度)，然后使托盘由静止释放，则刚释放托盘时，砝码对托盘的作用力等于
A. 2mgB. 3mg
C. 4mgD. 6mg
【答案】C
【解析】
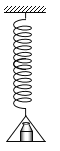
设弹簧劲度系数为k，托盘静止，弹簧伸长L时，以托盘及砝码整体为研究对象，受力平衡，有kL=3mg．伸长2L时，释放瞬间，以整体为研究对象，受力如图所示，则： 2kL-3mg=3ma，解得a=g．隔离砝码为研究对象，受力如图所示，则：N-2mg=2ma ，解得：N=4mg，据牛顿第三定律，砝码对托盘的作用力为4mg．故C项正确，ABD三项错误．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在“探究求合力的方法”实验中，现有木板、白纸、图钉、橡皮筋、细绳套、三角板和一把弹簧秤。
(1)为完成实验，某同学另找来一根弹簧，先测量其劲度系数，得到的实验数据如下表：
弹力F(N) | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
伸长量x(10-2m) | 0.74 | 1.80 | 2.80 | 3.72 | 4.60 | 5.58 | 6.42 |
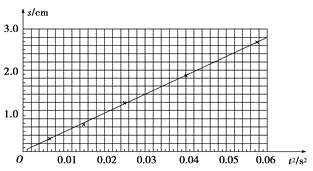
用作图法求得该弹簧的劲度系数k=________N/m；（保留两位有效数字）
_______
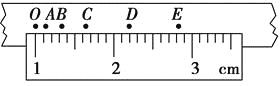
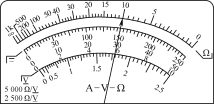
(2)某次实验中，图甲弹簧秤的指针位置如图所示，其读数为__________N；同时利用(1)中结果获得图甲左边弹簧上的弹力值为3.0 N，请在图乙用力的图示画出这两个共点力的合力F合；______
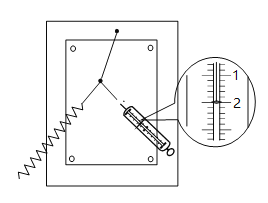
(3)由图得F合=__________N。
