题目内容
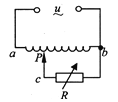
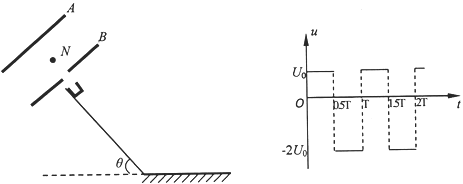
【题目】A和B是真空中的两块面积很大的平行金属板，B板中间开有小孔，两板间加上周期为T的交流电压u，如图所示，t=0时A板电势高于B板电势。在与A、B板距离均为L的N处能不断地产生电荷量为q、质量为m的带正电的微粒，微粒的初速度可视为零，重力不计。倾角为θ的绝缘斜面，底端与水平面平滑连接，斜面和水平面处在同一匀强磁场中，磁感应强度大小为B，磁场方向垂直纸面向外。斜面的顶端有一专门接收带电微粒的靶盒，开始时靶盒处于锁定状态，经过一段时间后靶盒内的电荷量达到nq时，N处不再产生带电微粒，此时将靶盒解锁，靶盒开始沿斜面下滑。已知斜面足够长，重力加速度大小为g，L2=
，靶盒的质量为M，靶盒与斜面和水平面间的动摩擦因数均为μ。
(1)求t=0时刻N处产生的微粒到达小孔的时间；
(2)若t0(t0<0.5T)时刻产生的微粒到达小孔时的速度恰好为零，求t0的值；
(3)靶盒在斜面上运动时达到的最大速度为多少?
(4)若靶盒在水平面上经过时间t3停止运动，求靶盒在水平面上运动的路程。
【答案】（1）
（2）
（3）
（4）
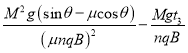
【解析】（1）设粒子加速的时间为t，则
， 
（或
）
由于
，故粒子一直做加速运动。
因此t=0时刻N处此时的微粒到达小孔的时间为
（2）粒子加速时间为
，减速时间为
，则
， 
联立解得
（或
）
（3）设最大速度为
，则达到最大速度时合力为零，故有
， 
， 
， 
，联立解得
（4）设靶盒在水平方向上运动的路程为s，t时刻靶盒的速度为v，
则根据动量定理可得
又因为
联立解得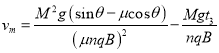
练习册系列答案
世纪百通期末金卷系列答案
相关题目
