题目内容
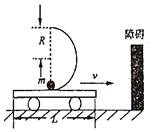
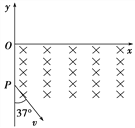
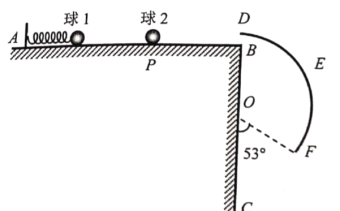
【题目】在光滑绝缘水平轨道上有一弹簧左端系于A点,右端与质量为3m的小球1接触但不连接。现用外力推动小球1将弹簧压缩至弹性势能为Ep=mgs(s为一定值)时静止释放,离开弹簧后与静止在P点质量为m、带电量为q(q>0)的小球2发生弹性正碰(不发生电荷转移),碰后小球2从DB进入圆弧轨道,如图所示。BC是一段竖直墙面,DEF是固定在竖直平面内的一段光滑绝缘圆弧轨道,轨道上端D点的切线水平,B、D间距很小,可看作重合的点。圆心O与轨道下端F的连线与竖直墙面的夹角为53°在BC右边整个空间有水平向左、场强E=
的匀强电场,小球2进入圆孤轨道之后恰好能沿着轨道DEF运动,一段时间后从轨道下端F处脱离,最后打在竖直墙面BC的C点。已知重力加速度为g,sin53°=0.8。
求：（1）碰后小球2运动的速度;
（2）轨道DEF的半径R;
（3）小球2打在C点前瞬间的速度。
【答案】（1）
（2）
（3）
【解析】
（1）由能量守恒得
①
1、2小球根据动量守恒得：
②.
1、2小球根据机械能守恒得：
③.
由①②③式解得：
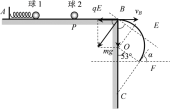
（2）由题意得：
.
设DEF轨道半径为R，设在E点小球达到等效最高点，由于小球恰好能沿着DEF轨道运动，则在E点有：
①.
根据动能定理得：
.②.
由①②式解得：
m
（3）过点F做切线以及垂直BC的水平线，则α为53°。又因为
，则小球所受合力的方向与水平方向夹角成53°。即在F点小球速度方向与合力方向共线，小球做直线运动。
由几何关系得：
m.
从B到C全程动能定理有：
解得：
.
练习册系列答案
相关题目
