题目内容
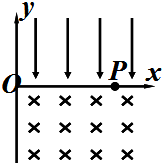 如图所示,在x轴上方有一匀强电场,场强为E,方向竖直向下.在x轴下方有一匀强磁场,磁感应强度为B,方向垂直纸面向里.在x轴上有一点P,离原点的距离为a.现有一带电量+q的粒子,质量为m,从静止开始释放,要使粒子能经过P点,其初始坐标应满足什么条件?(重力作用忽略不计)
如图所示,在x轴上方有一匀强电场,场强为E,方向竖直向下.在x轴下方有一匀强磁场,磁感应强度为B,方向垂直纸面向里.在x轴上有一点P,离原点的距离为a.现有一带电量+q的粒子,质量为m,从静止开始释放,要使粒子能经过P点,其初始坐标应满足什么条件?(重力作用忽略不计)分析:要使粒子从静止开始能经过P点,其初始位置必须在匀强电场区域里,由电场加速获得速度才能到达P点.题中P点的位置未知,分情况进行讨论:
1、若粒子从y轴上由静止释放,则粒子先加速后磁场偏转,由几何知识得到磁场中圆周运动的半径与OP距离间的关系:a=2nR (=n=1,2,3,…).分别根据动能定理和牛顿第二定律求解电场加速粒子获得的速度、磁场中轨迹半径表达式,即可求出初始坐标满足的条件;
2、若粒子在电场中的起点坐标为(x,y2),分x>a,x=a,x<a三种情况讨论,用同样的方法求解.
1、若粒子从y轴上由静止释放,则粒子先加速后磁场偏转,由几何知识得到磁场中圆周运动的半径与OP距离间的关系:a=2nR (=n=1,2,3,…).分别根据动能定理和牛顿第二定律求解电场加速粒子获得的速度、磁场中轨迹半径表达式,即可求出初始坐标满足的条件;
2、若粒子在电场中的起点坐标为(x,y2),分x>a,x=a,x<a三种情况讨论,用同样的方法求解.
解答:解:要使粒子能经过P点,其初始位置必须在匀强电场区域里.由于没有明确粒子所在的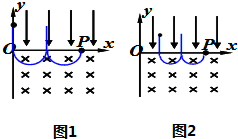 位置,分两种情况讨论:
位置,分两种情况讨论:
(1)若粒子从y轴上由静止释放,在电场加速下沿y轴从原点O进入磁场做半径为R的匀速圆周运动.由于粒子可能偏转一个、十个…半圆到达P点,由几何知识得
a=2nR (n=1,2,3,…) ①
设释放处距O的距离为y1,则有
qEy1=
mv2 ②
又 qvB=m
③
由①②③得,y1=
(n=1,2,3,…)
(2)若粒子在电场中的起点坐标为(x,y2)
据题意分析,有
若x>a,根据左手定则判断可知,粒子不可能经过P点;
若x=a,不论取值如何,粒子均能经过P点;
若x<a,则 a-x=2nR(n=1,2,3,…)
同理可得
y2=
(n=1,2,3,…)
答:要使粒子能经过P点,其初始坐标应满足条件是:
(1)若粒子从y轴上由静止释放,y1=
(n=1,2,3,…);
(2)若粒子在电场中的起点坐标为(x,y2),
x=a或x<a,y2=
(n=1,2,3,…).
 位置,分两种情况讨论:
位置,分两种情况讨论:(1)若粒子从y轴上由静止释放,在电场加速下沿y轴从原点O进入磁场做半径为R的匀速圆周运动.由于粒子可能偏转一个、十个…半圆到达P点,由几何知识得
a=2nR (n=1,2,3,…) ①
设释放处距O的距离为y1,则有
qEy1=
| 1 |
| 2 |
又 qvB=m
| v2 |
| R |
由①②③得,y1=
| B2qa2 |
| 8n2mE |
(2)若粒子在电场中的起点坐标为(x,y2)
据题意分析,有
若x>a,根据左手定则判断可知,粒子不可能经过P点;
若x=a,不论取值如何,粒子均能经过P点;
若x<a,则 a-x=2nR(n=1,2,3,…)
同理可得
y2=
| B2q(a-x)2 |
| 8n2mE |
答:要使粒子能经过P点,其初始坐标应满足条件是:
(1)若粒子从y轴上由静止释放,y1=
| B2qa2 |
| 8n2mE |
(2)若粒子在电场中的起点坐标为(x,y2),
x=a或x<a,y2=
| B2q(a-x)2 |
| 8n2mE |
点评:本题是多解问题,在条件不明时,要分情况进行讨论,不能漏解.分析时,要画出粒子运动的轨迹,根据几何关系得到粒子运动的半径与OP距离的关系是本题解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图所示,在x轴上方有匀强磁场B,一个质量为m,带电量为-q的粒子,以速度v从O点射入磁场,θ角已知,粒子重力不计,粒子在磁场中的运动时间为( )
如图所示,在x轴上方有匀强磁场B,一个质量为m,带电量为-q的粒子,以速度v从O点射入磁场,θ角已知,粒子重力不计,粒子在磁场中的运动时间为( ) 如图所示,在x轴上方有磁感应强度为B、方向垂直纸面向里的均匀磁场,x轴下方有电场为E、方向竖直向下的均匀电场,现有一质量为m、电量为q的粒子从y轴上某一点由静止开始释放,重力忽略不计,为使它能到达x轴上位置为x=L的一点Q,求:
如图所示,在x轴上方有磁感应强度为B、方向垂直纸面向里的均匀磁场,x轴下方有电场为E、方向竖直向下的均匀电场,现有一质量为m、电量为q的粒子从y轴上某一点由静止开始释放,重力忽略不计,为使它能到达x轴上位置为x=L的一点Q,求: 如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( )
如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( ) 如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场.一个不计重力的带电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角,若粒子从x轴上的P点射出磁场,已知p点与O点的距离为a,则该粒子的比荷和所带电荷的正负是( )
如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场.一个不计重力的带电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角,若粒子从x轴上的P点射出磁场,已知p点与O点的距离为a,则该粒子的比荷和所带电荷的正负是( ) 如图所示,在x轴上方(y≥0)存在着垂直于纸面向里的匀强磁场,磁感强度为B.在原点O有一离子源向x轴上方的各个方向发射出质量为m、电量为q的正离子,速率都为υ,对那些在xOy平面内运动的离子,在磁场中到达的最大x坐标和最大y坐标各是多少?
如图所示,在x轴上方(y≥0)存在着垂直于纸面向里的匀强磁场,磁感强度为B.在原点O有一离子源向x轴上方的各个方向发射出质量为m、电量为q的正离子,速率都为υ,对那些在xOy平面内运动的离子,在磁场中到达的最大x坐标和最大y坐标各是多少?