题目内容
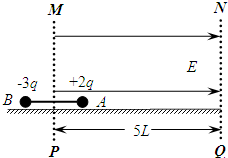（2009?上海模拟）在光滑绝缘的水平面上，用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B．A球的带电量为+2q，B球的带电量为-3q，组成一带电系统，如图所示，虚线MP为AB两球连线的垂直平分线，虚线NQ与MP平行且相距5L．最初A和B分别静止于虚线MP的两侧，距MP的距离均为L，且A球距虚线NQ的距离为4L．若视小球为质点，不计轻杆的质量，在虚线MP，NQ间加上水平向右的匀强电场E后，试求：（1）B球刚进入电场时，带电系统的速度大小；
（2）带电系统向右运动的最大距离；
（3）带电系统从开始运动到速度第一次为零时，B球电势能的变化量．
分析：（1）在B进入电场前只有A球受电场力2qE，根据动能定理列式求B球刚进入电场时系统的速度的大小v．
（2）B球进入电场后受到向左的电场力，系统向右做匀减速运动，当系统的速度为零时，向右运动的距离最大，根据动能定理列式求解；
（3）B球进入电场后电场力对B球所做的功W=-6qL，故B球电势能增加了6EqL．
（2）B球进入电场后受到向左的电场力，系统向右做匀减速运动，当系统的速度为零时，向右运动的距离最大，根据动能定理列式求解；
（3）B球进入电场后电场力对B球所做的功W=-6qL，故B球电势能增加了6EqL．
解答：解：（1）设带电系统开始运动时，系统的速度为v1
对A、B系统，应用动能定理得
2qEL=
2mv12
则得 v1=
（2）设球A向右运动s时，系统速度为零
对整个过程，A球电场力做功等于B球克服电场力做功，由动能定理得：
2qE×s-3qE×（s-L）=0，
则得s=3L
（3）B球进入电场距离为2L，B球克服电场力做功WFB=6qEL
则B球电势能增加了6qEL
答：
（1）B球刚进入电场时，带电系统的速度大小是
；
（2）带电系统向右运动的最大距离是3L；
（3）带电系统从开始运动到速度第一次为零时，B球电势能增加了6qEL．
对A、B系统，应用动能定理得
2qEL=
| 1 |
| 2 |
则得 v1=
|
（2）设球A向右运动s时，系统速度为零
对整个过程，A球电场力做功等于B球克服电场力做功，由动能定理得：
2qE×s-3qE×（s-L）=0，
则得s=3L
（3）B球进入电场距离为2L，B球克服电场力做功WFB=6qEL
则B球电势能增加了6qEL
答：
（1）B球刚进入电场时，带电系统的速度大小是
|
（2）带电系统向右运动的最大距离是3L；
（3）带电系统从开始运动到速度第一次为零时，B球电势能增加了6qEL．
点评：解决本题的过程中要注意在B球未进入电场和B球进入电场后系统所受的电场力不同，由于涉及电场力在空间的效果，优先考虑运用动能定理，也可以由牛顿第二定律和运动学公式结合求解．
练习册系列答案
相关题目
（2009?上海模拟）如图所示，质量为M=2kg的长木板上表面光滑，与水平地面的动摩擦因数为μ=0.2，在板上放有两个小物块，可看作质点，左边的小物块质量为 m1=1.5kg，距木板左端x1=8m，右边的小物块质量为m2=0.5kg，与m1的距离为x2=4m．现敲击木板左端使其瞬间获得10m/s向右的初速度．求：
（2009?上海模拟）如图所示，在一只烧瓶口插入一细玻璃管，管的另一端与一水银压强计相通，烧瓶中封闭着一定质量的理想气体，开始时气压计的U形管的两水银面一样高．现将瓶浸入热水中，改变烧瓶中气体的温度，则下面操作中正确的是（ ）
（2009?上海模拟）一质点自x轴原点O出发，沿正方向以加速度a运动，经过to时间速度变为v0，接着以-a加速度运动，当速度变为-
（2009?上海模拟）如图所示，铜棒ab长0.1m，质量为0.06kg，两端与长为0.15m的轻铜线相连，静止于竖直平面上，整个装置处在竖直向下的匀强磁场中，磁感应强度为B=0.5T，现接通电源，使铜棒中保持有恒定电流通过，铜棒发生摆动．已知最大偏转角为37°，则在摆到最大偏角的过程中铜棒的重力势能增加了