题目内容
如图所示，甲、乙两同学从河中O点出发，分别沿直线游到A点和B点后，立即沿原路线返回到O点．OA、OB分别与水流方向平行和垂直，且OA=OB=12m．若水流速度为1.5m/s不变，两人在静水中游速相等均为2.5m/s，他们所用时间分别用t甲、t乙表示，则（ ）分析：甲、乙两同学实际的速度是静水中的流速与水流速度的合速度，设游速为v，水速为v0根据速度合成可知：甲游到A点的速度为v+v0，游回的速度为v-v0；乙来回的速度都为
．明确了各自的合速度后，再用匀速直线运动规律求出时间进行比较．
v2-
|
解答：
解：设游速为v，水速为v0，OA=OB=l，
则甲整个过程所用时间：t 甲=
+
=
+
=15s，
乙为了沿OB运动，速度合成如图：
则乙整个过程所用时间：t乙=
×2=
×2=12s，故C正确，选项A、B、D错误．
故选：C．
解：设游速为v，水速为v0，OA=OB=l，则甲整个过程所用时间：t 甲=
| l |
| v+v0 |
| l |
| v-v0 |
| 12 |
| 2.5+1.5 |
| 12 |
| 2.5-1.5 |
乙为了沿OB运动，速度合成如图：
则乙整个过程所用时间：t乙=
| l | ||||
|
| 12 | ||
|
故选：C．
点评：本题考查运动的合成（主要是速度的合成）和匀速运动规律，运用速度合成的矢量平行四边形法则求出各自的合速度是关键．
练习册系列答案
相关题目
如图所示，甲、乙两运动员同时从水流湍急的河岸下水游泳，甲在乙的下游且速度大于乙．欲使两人尽快在河中相遇，则应选择的游泳方向是（ ）
如图所示为甲、乙两物体的v-t图象．甲、乙两物体从同一点沿同一直线运动，下列说法正确的是（ ）
如图所示是甲、乙两物体从同一点出发的运动图象，由图象可以看出在0～4s内（ ）
如图所示，甲、乙两个小球从同一同定斜面的顶端0点水平抛出，分别落到斜面上的A、B两点，A点为OB的中点，不计空气阻力．以下说法正确的是（ ）
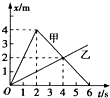如图所示是甲、乙两物体从同一点出发的位移-时间（x-t）图象，由图象可以看出在0～4s这段时间内（ ）| A、甲、乙两物体始终同向运动 | B、4 s时甲、乙两物体之间的距离最大 | C、甲的平均速度大于乙的平均速度 | D、甲、乙两物体之间的最大距离为3 m |