题目内容
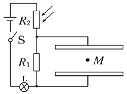
【题目】如图所示，MN、PQ两平行光滑水平导轨分别与半径r=0.5m的相同竖直半圆导轨在N、Q端平滑连接，M、P端连接定值电阻R，质量M=2kg的cd绝缘杆垂直静止在水平导轨上，在其右侧至N、Q端的区域内充满竖直向上的匀强磁场。现有质量m=1kg的ab金属杆以初速度v0=12m/s水平向右与cd绝缘杆发生正碰后，进入磁场并最终未滑出，cd绝缘杆则恰好能通过半圆导轨最高点，不计其它电阻和摩擦，ab金属杆始终与导轨垂直且接触良好，取g=10m/s2，求：
（1）cd绝缘杆通过半圆导轨最高点时的速度大小v；
（2）电阻R产生的焦耳热Q。
【答案】（1）
（2）
【解析】
根据cd恰好过最高点，可以求出cd碰后的速度，再根据动量守恒和能量守恒分析求解即可。
（1）cd绝缘杆通过半圆导轨最高点时，由牛顿第二定律有：
解得：
（2）碰撞后cd绝缘杆以速度
滑至最高点的过程中，由动能定理有：
解得：
由于cd是绝缘杆，所以不过电流，所以碰后一直匀速运动，
则碰撞后cd绝缘杆的速度：
两杆碰撞过程，动量守恒，有：
解得碰撞后ab金属杆的速度：
ab金属杆进入磁场后由能量守恒定律有：
解得：Q=2J
练习册系列答案
相关题目
