题目内容
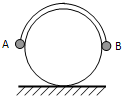 A、B两小球用细线相连,跨过固定的半径为R的光滑圆柱,圆柱固定在水平桌面的边缘,开始两球位置如图所示(AB在同一水平线上,且与圆心等高),松手后A球上升,B球下降,若A滑至最高点时速度恰好为
A、B两小球用细线相连,跨过固定的半径为R的光滑圆柱,圆柱固定在水平桌面的边缘,开始两球位置如图所示(AB在同一水平线上,且与圆心等高),松手后A球上升,B球下降,若A滑至最高点时速度恰好为| Rg |
分析:由于是光滑圆柱,两球从静止开始至A上升到圆柱的最高点过程中,A、B两小球作为整体机械能守恒,
根据机械能守恒表达式列出等式求解.
根据机械能守恒表达式列出等式求解.
解答:解:两球从静止开始至A上升到圆柱的最高点,
A与B组成的系统减少的势能为:
△Ep减=mbg?
-magR
根据系统机械能守恒得:
△Ep减=△Ek增
mbg?
-magR=
mav2+
mbv2,
v=
解得:ma:mb=(π-1):3.
答:A、B两小球质量之比为
.
A与B组成的系统减少的势能为:
△Ep减=mbg?
| 2πR |
| 4 |
根据系统机械能守恒得:
△Ep减=△Ek增
mbg?
| 2πR |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
v=
| Rg |
解得:ma:mb=(π-1):3.
答:A、B两小球质量之比为
| π-1 |
| 3 |
点评:该题主要考查了系统机械能守恒定律的应用,注意A和B上升和下降的距离不等.

练习册系列答案
相关题目
 用细线悬挂一个质量为m,带正电的小球,置于如图所示的匀强磁场中.当小球偏离竖直方向在垂直于磁场方向摆动时,如果细线始终绷紧,不计空气阻力,则前后两次通过最低点时相比较,相同的物理量是( )
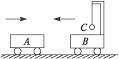
用细线悬挂一个质量为m,带正电的小球,置于如图所示的匀强磁场中.当小球偏离竖直方向在垂直于磁场方向摆动时,如果细线始终绷紧,不计空气阻力,则前后两次通过最低点时相比较,相同的物理量是( ) 小球A、B用轻弹簧相连接,再用细线吊起,剪断细线瞬间A球的加速度等于1.5g(g为重力加速度),则在剪断细线瞬间B球的加速度是
小球A、B用轻弹簧相连接,再用细线吊起,剪断细线瞬间A球的加速度等于1.5g(g为重力加速度),则在剪断细线瞬间B球的加速度是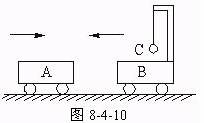
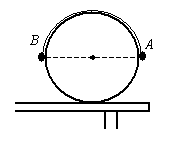 一个光滑的圆柱体固定在桌面上,圆柱体的半径为r。质量分别为mA和mB的两个小球A和B(都可看作质点,且mA>mB)用一根细线相连接,细线的长度恰好等于圆柱体的半个圆周长。开始时使两小球位于同一水平面上,如图所示,无初速地释放,求
一个光滑的圆柱体固定在桌面上,圆柱体的半径为r。质量分别为mA和mB的两个小球A和B(都可看作质点,且mA>mB)用一根细线相连接,细线的长度恰好等于圆柱体的半个圆周长。开始时使两小球位于同一水平面上,如图所示,无初速地释放,求