题目内容
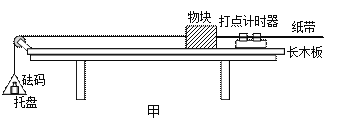
【题目】如图所示，真空中有一个半径为R的均匀透明介质球，一细束激光沿直线AB传播，在介质球表面的B点经折射进入球，入射角θ1＝60°，在球面上另一点又一次经折射后进人真空，此时激光的传播方向相对于光线AB偏转了60°.已知真空中的光速为c，求：
①介质球的折射率n；
②激光在介质球中传播的时间t.
【答案】(1) 
(2) 
【解析】试题分析：画出光路图，由几何知识得到激光束的折射角，由折射定律求出折射率；由几何知识求出BD的长度，由
出激光束在玻璃球中传播的速度，则可求出此激光束在玻璃中传播的时间。
①激光的光路图如图所示：
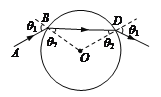
由几何关系可知折射角 θ2=30°
由折射定律有： 
解得： 
②激光在介质中传播的距离 
传播的速度 ： 
激光在介质球中传播的时间： 
练习册系列答案
相关题目
