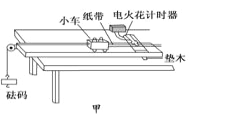
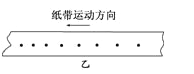
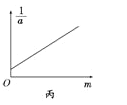
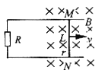
��Ŀ����
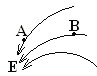
����Ŀ����ͼ��ʾһ�㹻���Ĺ⻬б�����Ϊ37��,б��AB��ˮƽ��BCƽ�����ӡ�����m=1 kg����Ϊ�ʵ����������ˮƽ���ϵ�D��,D���B��d=7 m,������ˮƽ���Ķ�Ħ������Ϊ0.4����ʹ�����ܵ�һˮƽ����ĺ���F=6.5 N����,��ʱ��t=2 s��ȥ����,���徭��B��ʱ�����ʲ���,�������ٶ�gȡ10 m/s2��sin 37��=0.6����

��1����ȥ����F��,���徭���ʱ�侭��B�㣿
��2���������ͣ�µ�λ�þ�B���Զ��
���𰸡���1��0.5s��2��1.125m
��������
��1��������ˮƽ�����˶������У��賷ȥFǰ������ļ��ٶȴ�С�ֱ�Ϊa1��a2
��ţ�ٵڶ����ɵ�F-��mg=ma1����ma=ma2
������a1��2.5m/s2��a2��4m/s2
����F����t=2sʱ�����λ��Ϊx1��![]() a1t2��
a1t2��![]() ��2.5��22m��5m
��2.5��22m��5m
��ʱ������ٶ�Ϊv=a1t=5m/s
�賷ȥ����F�������һ�ξ���B���ʱ��Ϊt1
����dx1��vt1![]() a1t12
a1t12
������t1=0.5s
���廬��B��ʱ�ٶȴ�СΪvB=v-a2t1=3m/s
��2�����廬��б����������˶����ٶȼ�Ϊ��ص�б�������Ϊб��⻬�������巵�ص�б���ʱ�ٶ���Ϊ3m/s��Ȼ��������ƽ�����������˶������ٶ���Ϊa2��4m/s2��������ͣ�µ�λ�þ�B��x��![]() ��1.125m
��1.125m

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�