Question

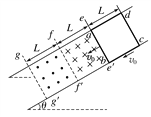
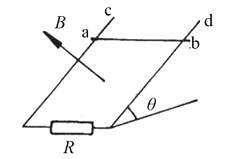
【题目】如图所示，两条足够长的平行的光滑裸导轨c、d所在斜面与水平面间夹角为θ，间距为L，导轨下端与阻值为R的电阻相连，质量为m的金属棒ab垂直导轨水平放置，整个装置处在垂直斜面向上的磁感应强度为B的匀强磁场中。导轨和金属棒的电阻均不计，有一个水平方向的力垂直作用在棒上，棒的初速度为零，则：（重力加速度为g）

（1）若金属棒中能产生从a到b的感应电流，则水平力F需满足什么条件？

（2）当水平力大小为F1，方向向右时，金属棒ab运动的最大速度vm是多少？

（3）当水平力方向向左时，金属棒ab沿轨道运动能达到的最大速度vm最大为多少？此时水平力F的大小为多大？

Answer 1

【答案】（1）（2） （3）；

【解析】

试题（1）金属棒中能产生从a到b的感应电流，说明金属棒沿导轨向上运动切割磁感线．分析其受力情况，由F沿斜面向的分力大于最大静摩擦力求解．（2）金属棒ab运动的速度最大时加速度为零，推导出安培力与速度的关系，再由平衡条件求解最大速度．要分情况讨论．（3）为使金属棒ab能沿导轨运动，恰好不脱离轨道，支持力为零，受力分析，由垂直于导轨方向的受力平衡求解．

（1）金属棒中能产生从a到b的感应电流，说明金属棒沿导轨向上运动切割磁感线．受力分析如图：

则有：

故：

（2）分情况讨论：受力分析如图．

若较大，金属棒将加速上滑，安培力平行于斜面向下，棒先加速后匀速，匀速时即为最大速度．

则有：

解得：

若较小，金属棒将加速下滑，安培力平行于斜面向上，棒先加速后匀速，匀速时即为最大速度．

则有：

解得：

（3）当水平力方向向左时，受力分析如图．

为使金属棒ab能沿导轨运动，恰好不脱离轨道，支持力为零，受力分析如图．

故有：

沿轨道向下滑动有最大速度时有：

当F为最大时，就最大，得到v最大

解得：F最大为，最大为

故速度的最大值为：

此时