题目内容
如图a所示,水平直线MN下方有竖直向上的匀强电场,现将一重力不计、比荷![]() =106 C/kg的正电荷置于电场中的O点由静止释放,经过
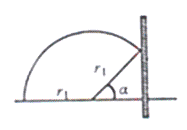
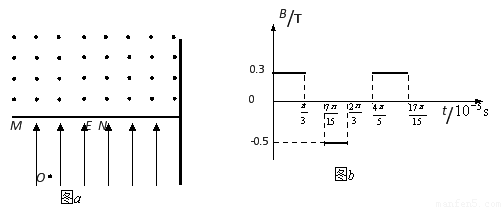
=106 C/kg的正电荷置于电场中的O点由静止释放,经过![]() ×10-5 s后,电荷以v0=1.5×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求:
×10-5 s后,电荷以v0=1.5×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求:
(1)匀强电场的电场强度E的大小; (保留2位有效数字)
(2)图b中t=![]() ×10-5 s时刻电荷与O点的水平距离;
×10-5 s时刻电荷与O点的水平距离;
(3)如果在O点右方d=68 cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间.(sin 37°=0.60,cos 37°=0.80) (保留2位有效数字)

解析:(15分)
⑴电荷在电场中做匀加速直线运动,设其在电场中运动的时间为![]() ,有:
,有:
![]()
![]()
解得:![]() (3分)
(3分)
⑵当磁场垂直纸面向外时,电荷运动的半径:
![]()
周期 ![]() (1分)
(1分)
当磁场垂直纸面向里时,电荷运动的半径:
![]()
周期 ![]() (1分)
(1分)
故电荷从t=0时刻开始做周期性运动,其运动轨迹如图所示。
![]() 时刻电荷与O点的水平距离:Δd=
时刻电荷与O点的水平距离:Δd=![]() =4cm (3分)
=4cm (3分)
⑶电荷从第一次通过MN开始,其运动的周期为:![]()
根据电荷的运动情况可知,电荷到达档板前运动的完整周期数为15个,有:
电荷沿ON运动的距离:s=15Δd=60cm (1分)
故最后8cm的距离如图所示,有:
![]()
解得:![]() 则
则![]() (3分)
(3分)
故电荷运动的总时间:
![]() ((3分)
((3分)


 阅读快车系列答案
阅读快车系列答案





 的正电荷置于电场中的O点由静止释放,经过
的正电荷置于电场中的O点由静止释放,经过 后,电荷以v0=l.5 ×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图6所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求:
后,电荷以v0=l.5 ×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图6所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求:
 时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离; 取3.14,计算结果保留三位有效数字)
取3.14,计算结果保留三位有效数字)