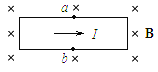题目内容
【题目】电磁弹射在电磁炮、航天器、舰载机等需要超高速的领域中有着广泛的应用，图1所示为电磁弹射的示意图。为了研究问题的方便，将其简化为如图2所示的模型（俯视图）。发射轨道被简化为两个固定在水平面上、间距为L且相互平行的金属导轨，整个装置处于竖直向下、磁感应强度为B的匀强磁场中。发射导轨的左端为充电电路，已知电源的电动势为E，电容器的电容为C，子弹载体被简化为一根质量为m、长度也为L的金属导体棒，其电阻为r。金属导体棒，其电阻为r。金属导体棒垂直放置于平行金属导轨上，忽略一切摩擦阻力以及导轨和导线的电阻。
（1）发射前，将开关S接a，先对电容器进行充电。
a．求电容器充电结束时所带的电荷量Q；
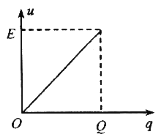
b．充电过程中电容器两极板间的电压y随电容器所带电荷量q发生变化。请在图3中画出u-q图像；并借助图像求出稳定后电容器储存的能量E0；
（2）电容器充电结束后，将开关b，电容器通过导体棒放电，导体棒由静止开始运动，导体棒离开轨道时发射结束。电容器所释放的能量不能完全转化为金属导体棒的动能，将导体棒离开轨道时的动能与电容器所释放能量的比值定义为能量转化效率。若某次发射结束时，电容器的电量减小为充电结束时的一半，不计放电电流带来的磁场影响，求这次发射过程中的能量转化效率
。
【答案】（1）a．
；b．
；
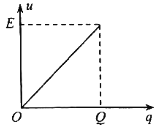（2）
【解析】
（1）a、根据电容的定义
电容器充电结束时其两端电压U等于电动势E，解得电容器所带电荷量
b、根据以上电容的定义可知
，画出q-u图像如图所示：
有图像可知，稳定后电容器储存的能量
为图中阴影部分的面积
，
将Q代入解得
（2）设从电容器开始放电至导体棒离开轨道时的时间为t，放电的电荷量为
，平均电流为
，导体棒离开轨道时的速度为v
根以导体棒为研究对象，根据动量定理
，（或
），
据电流定义可知
（或
）
根据题意有
，联立解得
导体棒离开轨道时的动能
电容器释放的能量
联立解得能量转化效率
黄冈创优卷系列答案
