题目内容
如图所示．在竖直平面内有轨道ABCDE，其中BC是半径为R的四分之一圆弧轨道，AB(AB>R)是竖直轨道，CE是水平轨道，CD>R．AB与BC相切于B点，BC与CE相切于C点，轨道的AD段光滑，DE段粗糙且足够长。一根长为R的轻杆两端分别固定着两个质量均为m的相同小球P、Q(视为质点)，将轻杆锁定在图示位置，并使Q与B等高。现解除锁定释放轻杆，轻杆将沿轨道下滑，重力加速度为g。
(1)Q球经过D点后，继续滑行距离s停下(s>R)．求小球与DE段之间的动摩擦因数。
(2)求Q球到达C点时的速度大小。
解析：(1)分析滑行过程如图所示
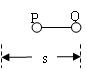
由能量守恒得mgR+mg2R=μmgs+μmg(s-R)
解得
(2)轻杆由释放到Q球到达C点时，系统的机械能守恒，设P、Q两球的速度大小分别为vP，vQ，则
又vP=vQ 1分
联立解得
练习册系列答案
阅读快车系列答案
相关题目
（2008?广州二模）如图所示，在竖直平面内有水平向右的匀强电场，同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球，另一端固定于0点，已知带电小球受到的电场力大于重力，小球由静止释放，到达图中竖直虚线前小球做（ ）
如图所示，在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中，电场方向与正方形一边平行．一质量为m、带电量为q的小球由某一边的中点，以垂直于该边的水平初速V0进入该正方形区域．当小球再次运动到该正方形区域的边缘时，具有的动能可能为（ ）
如图所示，在竖直平面内有一半圆形轨道，圆心为O，一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出，落于圆轨道上的C点，已知OC的连线与OA的夹角为θ，求小球从A到C的时间t=？（空气阻力不计）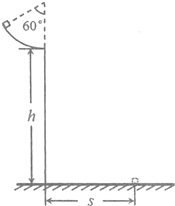
如图所示，在竖直平面内有一个粗糙的
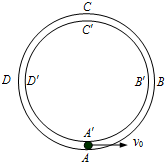如图所示，在竖直平面内固定两个很靠近的同心圆形轨道，外轨道ABCD光滑，内轨道A′B′C′D′的上半部分B′C′D′粗糙，下半部分B′A′D′光滑，一质量m=0.2kg的小球从轨道的最低点A，以初速度v0向右运动，球的尺寸略小于两圆间距，已知圆形轨道的半径R=0.32m，取g=10m/s2．