题目内容
如图,半径为R的光滑圆形轨道安置在一竖直平面上,左侧连接一个光滑的弧形轨道,右侧连接动摩擦因数为μ的水平轨道CD.一小球自弧形轨道上端的A处由静止释放,通过圆轨道后,再滑上CD轨道.若在圆轨道最高点B处对轨道的压力恰好为零,到达D点时的速度为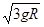 . 求:
. 求:

⑴小球经过B点时速度的大小.
⑵小球释放时的高度h.
⑶水平轨道CD段的长度l.
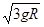 . 求:
. 求:
⑴小球经过B点时速度的大小.
⑵小球释放时的高度h.
⑶水平轨道CD段的长度l.
(1)vB=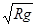 (2)
(2) (3)
(3)
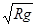 (2)
(2) (3)
(3)
试题分析:⑴根据小球在B处对轨道压力为零,由向心力公式有
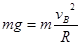 ① (2分)
① (2分)解得小球、经过B点时速度大小vB=
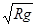 ②(2分)
②(2分)⑵取轨道最低点为零势能点,由机械能守恒定律
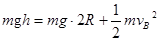 ③ (2分)
③ (2分)由②、③联立解得
 ④(2分)
④(2分)⑶对小球从最高点到D点全过程应用动能定理有
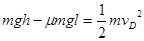 ⑤(2分)
⑤(2分)又vD=
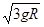 ⑥
⑥ 由④⑤⑥联立解得水平轨道CD段的长度
 (2分)
(2分)点评:掌握向心力公式外,还熟悉了牛顿第二定律,最后比较了机械能守恒定律与动能定理的优缺点.本题中小球在轨道最高点压力为零是解题的切入点.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目


 N
N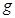 ,求:
,求:
 =2.0×103kg,发动机的额定输出功率为80kW,行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动,加速度的大小为
=2.0×103kg,发动机的额定输出功率为80kW,行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动,加速度的大小为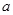 =1.0m/s2。达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶。试求:
=1.0m/s2。达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶。试求: