Question

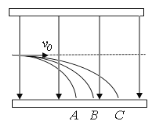
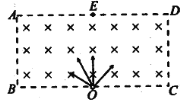
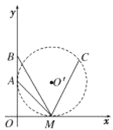
【题目】如图所示，在竖直平面内建立直角坐标系xOy，该平面内有AM、BM、CM三条光滑固定轨道，其中A、C两点处于同一个圆上，C是圆上任意一点，A、M分别为此圆与y、x轴的切点。B点在y轴上且∠BMO=60°，O′为圆心。现将a、b、c三个小球分别从A、B、C点同时由静止释放，它们将沿轨道运动到M点，所用时间分别为tA、tB、tC，则tA、tB、tC大小关系是（　　）

A.tB＞tC＞tA

B.tB=tC＞tA

C.tA=tB=tC

D.tB＞tA=tC

Answer 1

【答案】D

【解析】

考查牛顿第二定律的应用，等时圆法。

设⊙O′的半径为R，根据几何知识可知：

OA=OM=R

由勾股定理得：

即小球沿AM运动的位移为：

由牛顿第二定律得：

解得：

由:

得小球沿AM运动的时间为：

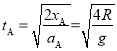
根据几何知识可知：

即小球沿BM运动的位移为：

由牛顿第二定律得：

解得：

小球沿BM运动的时间：

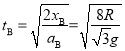
设CM与x轴正向的夹角为θ，由几何关系可知：

即小球沿CM运动的位移为：

由牛顿第二定律得：

解得：

小球沿CM运动的时间为：

则tA、tB、tC大小关系是：tB＞tA=tC，D正确，ABC错误。

故选D。