题目内容
【题目】如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直底端分别与两侧的直轨道相切,半径R=0.5m。物块A以某一速度滑入圆轨道,滑过最高点Q,再沿圆轨道滑出后,与直轨道上P处静止的物块B发生弹性碰撞,P点左侧轨道光滑,右侧轨道呈粗糙段、光滑段交替排列,每段长度都为L=0.1m,物块与各粗糙段间的动摩擦因数都为μ=0.5,A、B的质量均为m=1kg(重力加速度g取10m/s2;A、B视为质点,碰撞时间极短,有阴影的地方代表粗糙段),碰后B最终停止在第100个粗糙段的末端。求:
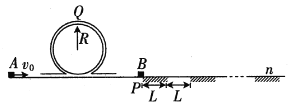
(1)A刚滑入圆轨道时的速度大小v0;
(2)A滑过Q点时受到的弹力大小F;
(3)碰后B滑至第n个(n<100)光滑段上的速度vn与n的关系式。
【答案】(1)10m/s;(2)150N;(3)vn=![]() m/s,(k
m/s,(k![]() 100)
100)
【解析】
(1)先求出滑块每经过一段粗糙段损失的机械能![]() E,进而求得损失的总能量,根据动量守恒和和能量守恒可得A刚滑入圆轨道时的速度大小v0。(2)在最高点Q由机械能守恒求得速度,由牛顿第二定律可得弹力F。(3)算出B滑到第n个光滑段前已经损失的能量,由能量守恒得速度vn与k的关系式。
E,进而求得损失的总能量,根据动量守恒和和能量守恒可得A刚滑入圆轨道时的速度大小v0。(2)在最高点Q由机械能守恒求得速度,由牛顿第二定律可得弹力F。(3)算出B滑到第n个光滑段前已经损失的能量,由能量守恒得速度vn与k的关系式。
(1)滑块每经过一段粗糙段损失的机械能![]() E=
E=![]() mgL,解得
mgL,解得![]() E=0.5J
E=0.5J
设碰后B的速度为vB,由能量关系有:![]() mvB2=100
mvB2=100![]() E
E
设碰后A的速度为vA,A、B碰撞为弹性碰撞,根据动量守恒和和能量守恒有:
mv0=mvA+mvB
![]() mv02=
mv02=![]() mvA2+
mvA2+![]() mvB2
mvB2
解得A刚滑入圆轨道时的速度大小v0=10m/s
(2)从A刚滑入轨道到最高点Q,由机械能守恒有:
![]() mv02=mg
mv02=mg![]() 2R+
2R+![]() mv2
mv2
在Q点根据牛顿第二定律得:F+mg=m![]()
解得A滑过Q点时受到的弹力大小F=150N
(3)B滑到第n个光滑段前已经损失的能量E损=k![]() E
E
由能量守恒有:![]() mvB2-
mvB2-![]() mvn=k
mvn=k![]() E
E
解得碰后B滑至第n个(n<100)光滑段上的速度vn与k的关系式:vn=![]() m/s,(k
m/s,(k![]() 100)
100)