题目内容
 如图所示,一小球从静止沿斜面以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=12m,AC=32m,小球通过AB、BC所用的时间均为2s,则:
如图所示,一小球从静止沿斜面以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=12m,AC=32m,小球通过AB、BC所用的时间均为2s,则:(1)求出小球下滑时的加速度?
(2)斜面A点以上部分至少有多长?
分析:小球沿斜面向下做匀加速直线运动,根据推论△x=aT2求出加速度,用推论求出小球经过B点时的瞬时速度,由速度位移关系求出斜面A点以上部分的长度.
解答:解:小球沿斜面向下做匀加速直线运动,则有
BC-AB=aT2
得到 a=
=
=
m/s2=2m/s2
小球经过B点时的瞬时速度为vB=
=
m/s=8m/s
设斜面A点以上部分至少为x.
则由
=2a(x+AB)
代入解得x=4m
答:
(1)求出小球下滑时的加速度2m/s2.
(2)斜面A点以上部分至少有4m.
BC-AB=aT2
得到 a=
| BC-AB |
| T2 |
| (AC-AB)-AB |
| T2 |
| 32-2×12 |
| 22 |
小球经过B点时的瞬时速度为vB=
| AC |
| 2T |
| 32 |
| 2×2 |
设斜面A点以上部分至少为x.
则由
| v | 2 B |
代入解得x=4m
答:
(1)求出小球下滑时的加速度2m/s2.
(2)斜面A点以上部分至少有4m.
点评:本题关键在于匀变速直线运动两大推论的应用.也可以运用基本公式列方程组求解.中等难度.

练习册系列答案
相关题目
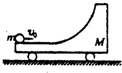 (2009?湖北模拟)右端带有l/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度vo水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )
(2009?湖北模拟)右端带有l/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度vo水平冲上小车,关于小球此后的运动情况,以下说法正确的是( ) (2012?南宁模拟)如图所示,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面:b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,a能离地面的最大高度为( )
(2012?南宁模拟)如图所示,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面:b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,a能离地面的最大高度为( ) 如图所示,一不可伸长的柔软轻绳跨过光滑的定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b,则当b刚落地时a的速度为( )
如图所示,一不可伸长的柔软轻绳跨过光滑的定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b,则当b刚落地时a的速度为( ) 如图所示,一平行板电容器水平放置,板内有竖直方向的匀强电场,板间距为d=0.4m,两块板上分别有一个小孔在同一竖直方向上,有一个带负电金属小球A质量为2m,电量为
如图所示,一平行板电容器水平放置,板内有竖直方向的匀强电场,板间距为d=0.4m,两块板上分别有一个小孔在同一竖直方向上,有一个带负电金属小球A质量为2m,电量为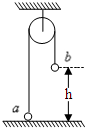 如图所示,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳的两端各系一小球a和b.a球质量为m,静置于地面;b球质量为M,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,a可能达到的最大高度为
如图所示,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳的两端各系一小球a和b.a球质量为m,静置于地面;b球质量为M,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,a可能达到的最大高度为