题目内容
 如图所示,一平行板电容器水平放置,板内有竖直方向的匀强电场,板间距为d=0.4m,两块板上分别有一个小孔在同一竖直方向上,有一个带负电金属小球A质量为2m,电量为
如图所示,一平行板电容器水平放置,板内有竖直方向的匀强电场,板间距为d=0.4m,两块板上分别有一个小孔在同一竖直方向上,有一个带负电金属小球A质量为2m,电量为-2q,静止于两小孔正中间.另有一带正电与A球大小相同的小球B,质量为m,电量为q,由上板小孔的正上方h=d=0.4m处,静止释放,不计阻力及小球间的静电力,小球下落进入电场后与A球发生正碰,碰撞时间极短,碰后A、B电量相同,A球速度为2.5m/s,求碰后B球经多长时间从小孔离开?B球从哪个板离开?(g=10m/s2)
分析:由题意可知小球A的重力与电场力相等,B球下落到与A碰过程,根据动能定理求出碰撞前的速度.
根据动量守恒求出碰撞后A、B的速度,
对B进行受力分析,运用牛顿第二定律和运动学公式求解.
根据动量守恒求出碰撞后A、B的速度,
对B进行受力分析,运用牛顿第二定律和运动学公式求解.
解答:解:由于A球平衡,则:2mg=2Eq
∴mg=Eq,电场强度方向向下
B球下落到与A碰过程,根据动能定理mgh+mg
=
mv12
∴v1=4m/s
A、B碰,动量守恒得:
mv1=mv′1+mv′2
v′2=2.5m/s v′1=-1m/s 反弹
碰后电量各为q=
=-
设B球反弹上升的最大高度为h
B球:mg-E
=ma
a=5m/s2,方向向下
B球向上做匀减速v0=-v′1=m/s
h=
=0.1m<
∴B球从下板离开
-
=v0t-
at2
∴t=
=0.55s
答:碰后B球经0.55s从小孔离开,B球从下板离开.
∴mg=Eq,电场强度方向向下
B球下落到与A碰过程,根据动能定理mgh+mg
| d |
| 2 |
| 1 |
| 2 |
∴v1=4m/s
A、B碰,动量守恒得:
mv1=mv′1+mv′2
v′2=2.5m/s v′1=-1m/s 反弹
碰后电量各为q=
| -2q+q |
| 2 |
| q |
| 2 |
设B球反弹上升的最大高度为h
B球:mg-E
| q |
| 2 |
a=5m/s2,方向向下
B球向上做匀减速v0=-v′1=m/s
h=
| ||
| 2a |
| d |
| 2 |
∴B球从下板离开
-
| d |
| 2 |
| 1 |
| 2 |
∴t=
1+
| ||
| 5 |
答:碰后B球经0.55s从小孔离开,B球从下板离开.
点评:解答中要注意通过分析得出主要的运动过程,再由题目给出的条件列式计算出我们需要的数据;本题对学生的分析问题能力要求较高,是道好题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
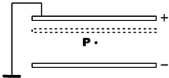 如图所示,一平行板电容器充电后与电源断开,正极板接地,在两极板间有一个负点电荷在P点恰好平衡.若用U表示两极板间的电压、E表示极板间的场强,并令负极板保持不动,而将正极板向下移到图中的虚线位置,则( )
如图所示,一平行板电容器充电后与电源断开,正极板接地,在两极板间有一个负点电荷在P点恰好平衡.若用U表示两极板间的电压、E表示极板间的场强,并令负极板保持不动,而将正极板向下移到图中的虚线位置,则( )| A、E增大,U减小 | B、E不变,U增大 | C、E增大,电荷有向上的加速度 | D、E不变,电荷电势能变小 |
 (2007?苏州二模)如图所示,一平行板电容器充电后与电源断开,负极板接地,在两极板间有一正电荷(电量很小)固定在P点.用E表示电容器两极板间的场强,U表示电容器两极板间的电压,ε表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( )
(2007?苏州二模)如图所示,一平行板电容器充电后与电源断开,负极板接地,在两极板间有一正电荷(电量很小)固定在P点.用E表示电容器两极板间的场强,U表示电容器两极板间的电压,ε表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( ) 如图所示,一平行板电容器充电后与电源断开,这时电容器的带电量为Q,P是电容器内一点,电容器的上板与大地相连,下列说法正确的是( )
如图所示,一平行板电容器充电后与电源断开,这时电容器的带电量为Q,P是电容器内一点,电容器的上板与大地相连,下列说法正确的是( ) 如图所示,一平行板电容器,上极板带正电下极板带负电,中间充满垂直于纸面向里的匀强磁场.一带电粒子a(不计重力)以一定的初速度由左边界的O点射入电容器,恰好沿直线从区域右边界的O′点(图中未标出)穿出.若撤去该区域内的磁场而其他条件均不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b( )
如图所示,一平行板电容器,上极板带正电下极板带负电,中间充满垂直于纸面向里的匀强磁场.一带电粒子a(不计重力)以一定的初速度由左边界的O点射入电容器,恰好沿直线从区域右边界的O′点(图中未标出)穿出.若撤去该区域内的磁场而其他条件均不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b( ) (2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )
(2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )