Question

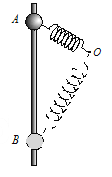
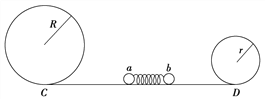
【题目】如图所示，半径分别为R＝1 m和r＝0.5 m的甲、乙两光滑圆轨道置于同一竖直平面内，两轨道之间由一段光滑水平轨道CD相连，在水平轨道CD上一轻弹簧被a、b两小球夹住，现同时由静止释放两小球，重力加速度取g＝10 m/s2.

①如果a、b小球都恰好能够通过各自圆轨道的最高点，求两小球的质量之比；

②如果a、b小球的质量均为0.5 kg，为保证两小球都能够通过各自圆轨道的最高点，求释放两小球前弹簧弹性势能的最小值．

【答案】(1) (2)

【解析】根据牛顿第二定律得出最高点的速度，根据机械能守恒定律，动量守恒定律列出等式求解；由动量守恒定律知两小球与弹簧分离时速度大小相等，再根据机械能守恒定律求解．

已知a、b小球恰好能通过各自圆轨道的最高点，则它们通过最高点时的速度大小分别为，

设两小球与弹簧分离时的速度大小分别为 ，根据动量守恒定律有

根据机械能守恒定律有，，。联立以上各式解得

②若ma=mb=0.5 kg，由动量守恒定律知两小球与弹簧分离时速度大小相等

当a小球恰好能通过最高点时，b小球一定也能通过最高点，a小球通过最高点的速度为，此时弹簧的弹性势能最小，最小值为

【点睛】解决该题关键能判断出小球能通过最高点的条件，然后根据动量守恒定律和机械能守恒定律联立列式求解。

【题型】解答题
【结束】
93

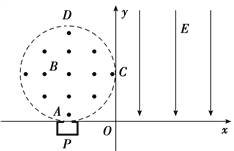
【题目】如图所示，在第一象限内有沿y轴负方向的电场强度大小为E的匀强电场．在第二象限中，半径为R的圆形区域内存在垂直纸面向外的匀强磁场，圆形区域与x、y轴分别相切于A、C两点．在A点正下方有一个粒子源P，P可以向x轴上方各个方向射出速度大小均为v0、质量为m、电荷量为＋q的带电粒子(重力不计，不计粒子间的相互作用)，其中沿y轴正向射出的带电粒子刚好从C点垂直于y轴进入电场．

(1)求匀强磁场的磁感应强度大小B.

(2)求带电粒子到达x轴时的横坐标范围和带电粒子到达x轴前运动时间的范围．

(3)如果将第一象限内的电场方向改为沿x轴负方向，分析带电粒子将从何处离开磁场，可以不写出过程．

Answer 1

【答案】(1) (2)x的范围，t的范围 (3)从A点正上方的D点离开磁场

【解析】试题分析:由题设条件，从A点沿y轴正方向射出的带电粒子刚好从C点垂直于y轴进入电场，由几何关系知道它做匀速圆周运动的半径为R，再由洛仑兹力提供向心力可以求得磁感应强度的大小；由于所有粒子做匀速圆周运动的半径等于磁场圆的半径，可以证明：沿不同方向进入磁场的带电粒子离开磁场时方向均沿x轴正方向进入电场，之后做类平抛运动，显然运动时间最长的带电粒子是从D点水平射出的粒子，由类平抛运动运动规律就能求出打在x轴的最远点；若将第一象限的电场改为沿x轴负方向，则粒子从磁场水平射出后做匀减速直线运动至速度为零，再沿x轴负方向做匀加速直线运动进入磁场做匀速圆周运动，由于速度方向反向，则粒子所受洛仑兹力反向，最后从D点射出磁场.

(1)带电粒子在磁场中做匀速圆周运动，从A点运动到C点的过程中带电粒子的运动轨迹为个圆弧，轨迹半径r=R

由，得

(2)沿不同方向进入磁场的带电粒子离开磁场时的速度大小均为v0，方向均平行于x轴，其临界状态为粒子从D点沿x轴正方向离开磁场

分析粒子从D点离开磁场的情况，粒子在磁场中运动时间为，得

从D点平行于x轴运动至y轴的时间

在第一象限内运动过程中，粒子做类平抛运动，设运动时间为t3，则，，

解得，

则

带电粒子到达x轴时的横坐标范围为

到达x轴前运动时间的范围

(3)将第一象限内的电场方向改为沿x轴负方向时，带电粒子将从A点正上方的D点离开磁场。