题目内容
13. 在一次国际城市运动会中,要求运动员从高为H的平台上A点由静止出发,沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出,最后落在水池中,如图所示.设滑道的水平距离为L,B点的高度h可由运动员自由调节(取g=10m/s2).求:
在一次国际城市运动会中,要求运动员从高为H的平台上A点由静止出发,沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出,最后落在水池中,如图所示.设滑道的水平距离为L,B点的高度h可由运动员自由调节(取g=10m/s2).求:(1)运动员到达B点的速度与高度h的关系;
(2)运动员要求到最大水平运动距离,B点的高度h应调为多大?
(3)对应的最大水平距离Xmax为多少?
分析 清楚运动员的运动过程,可运用动能定理研究A到B得过程把运动员到达B点的速度与高度h的关系联系起来.
求s的最大值,方法是把这个s先通过平抛运动规律表示出来,通过数学函数知识(可以配方)求极值.
解答 解:(1)设AB与水平面夹角为θ,A运动到B过程,摩擦阻力做功为:
Wf=μmgcosθ$\frac{L}{cosθ}$=μmgL
由A运动到B过程应用动能定理有:
mg(H-h)-μmgL=$\frac{1}{2}$mvB2-0
得:vB=$\sqrt{2g(H-h-μL)}$
(2、3)离开B点做平抛运动
竖直方向:h=$\frac{1}{2}$gt2
解得:t=$\sqrt{\frac{2h}{g}}$.
水平方向:x=vBt
解得:x=2$\sqrt{(H-h-μL)h}$=$2\sqrt{-{h}^{2}+(H+μL)h}$
当h=$\frac{H+μL}{2}$时,x有最大值,xmax=H-μL
所以对应的最大水平距离为Xmax=H-μL+L.
答:(1)运动员到达B点的速度与高度h的关系是vB=$\sqrt{2g(H-h-μL)}$;
(2)运动员要求到最大水平运动距离,B点的高度h应调为$2\sqrt{-{h}^{2}+(H+μL)h}$;
(3)对应的最大水平距离Xmax为H-μL+L.
点评 第一问中也可以用牛顿第二定律结合运动学公式求解,哪个简便你可以去尝试比较.
求一个物理量的极值,常见的方法是把这个物理量先表示出来,通过数学知识(可以配方)求极值.

练习册系列答案
相关题目
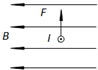
1. 如图所示,在水平面上有一固定的U形金属框架,框架上置一金属杆ab.在垂直纸面方向有一匀强磁场,下面情况电流方向判断正确的是( )
如图所示,在水平面上有一固定的U形金属框架,框架上置一金属杆ab.在垂直纸面方向有一匀强磁场,下面情况电流方向判断正确的是( )
 如图所示,在水平面上有一固定的U形金属框架,框架上置一金属杆ab.在垂直纸面方向有一匀强磁场,下面情况电流方向判断正确的是( )
如图所示,在水平面上有一固定的U形金属框架,框架上置一金属杆ab.在垂直纸面方向有一匀强磁场,下面情况电流方向判断正确的是( )| A. | 若磁场方向垂直纸面向外,并且磁感应强度增大时,b→a | |
| B. | 若磁场方向垂直纸面向外,并且磁感应强度减小时,b→a | |
| C. | 若磁场方向垂直纸面向里,并且ab向右移动时,a→b | |
| D. | 若磁场方向垂直纸面向里,并且ab向左移动时,b→a |
8. 如图所示是一列沿x轴正方向传播的简谐横波在t=0刻的波形图,已知波的传播速度v=2.0m/s.下列说法正确的是( )
如图所示是一列沿x轴正方向传播的简谐横波在t=0刻的波形图,已知波的传播速度v=2.0m/s.下列说法正确的是( )
 如图所示是一列沿x轴正方向传播的简谐横波在t=0刻的波形图,已知波的传播速度v=2.0m/s.下列说法正确的是( )
如图所示是一列沿x轴正方向传播的简谐横波在t=0刻的波形图,已知波的传播速度v=2.0m/s.下列说法正确的是( )| A. | x=0.5m处质点在0.5s内通过路程为5cm | |
| B. | x=1.0m处质点做简谐运动的表达式为y=5sin2πtcm | |
| C. | x=1.5m处质点在t=0时刻有正向最大加速度 | |
| D. | x=2.0m处质点经1s向x轴正向移动2m |
18.短跑运动员在百米竞赛中,测得5s末的速度为9.0m/s,10s末到达终点时的速度为11.2m/s,则运动员在全程内的平均速度为( )
| A. | 9.0m/s | B. | 11.2m/s | C. | 10.0m/s | D. | 10.1m/s |
3. 如图所示,位于粗糙固定斜面上的小物块P受到一水平向右的推力F的作用,现保持F的方向不变,使其减小,则物块所受静摩擦力(已知物块P始终保持静止).( )
如图所示,位于粗糙固定斜面上的小物块P受到一水平向右的推力F的作用,现保持F的方向不变,使其减小,则物块所受静摩擦力(已知物块P始终保持静止).( )
 如图所示,位于粗糙固定斜面上的小物块P受到一水平向右的推力F的作用,现保持F的方向不变,使其减小,则物块所受静摩擦力(已知物块P始终保持静止).( )
如图所示,位于粗糙固定斜面上的小物块P受到一水平向右的推力F的作用,现保持F的方向不变,使其减小,则物块所受静摩擦力(已知物块P始终保持静止).( )| A. | 一定变小 | B. | 一定变大 | ||
| C. | 一定不变 | D. | 可能变小,也可能变大 |
 如图所示,M、N为加速电场的两极板,M板中心有一小孔Q,其正上方有一半径为R1=1m的圆形磁场区域,圆心为0,另有一内半径为R1,外半径为R2=$\sqrt{3}$m的同心环形磁场区域,区域边界与M板相切于Q点,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一比荷$\frac{q}{m}$=4×107C/kg带正电粒子从N板的P点由静止释放,经加速后通过小孔Q,垂直进入环形磁场区域.已知点P、Q、O在同一竖直线上,不计粒子的重力,且不考虑粒子的相对论效应.
如图所示,M、N为加速电场的两极板,M板中心有一小孔Q,其正上方有一半径为R1=1m的圆形磁场区域,圆心为0,另有一内半径为R1,外半径为R2=$\sqrt{3}$m的同心环形磁场区域,区域边界与M板相切于Q点,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一比荷$\frac{q}{m}$=4×107C/kg带正电粒子从N板的P点由静止释放,经加速后通过小孔Q,垂直进入环形磁场区域.已知点P、Q、O在同一竖直线上,不计粒子的重力,且不考虑粒子的相对论效应.
 正方形金属线框abcd,每边长l=0.1m,总质量m=0.1kg,回路总电阻R=0.02Ω,用细线吊住,线的另一端跨过两个定滑轮,挂着一个质量为M=0.14kg的砝码.线框上方为一磁感应强度B=0.5T的匀强磁场区,如图,线框abcd在砝码M的牵引下做加速运动,当线框上边ab进入磁场后立即做匀速运动.接着线框全部进入磁场后又做加速运动(g=10m/s2).问:
正方形金属线框abcd,每边长l=0.1m,总质量m=0.1kg,回路总电阻R=0.02Ω,用细线吊住,线的另一端跨过两个定滑轮,挂着一个质量为M=0.14kg的砝码.线框上方为一磁感应强度B=0.5T的匀强磁场区,如图,线框abcd在砝码M的牵引下做加速运动,当线框上边ab进入磁场后立即做匀速运动.接着线框全部进入磁场后又做加速运动(g=10m/s2).问: