Question

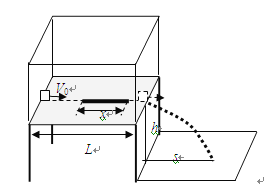
【题目】如图所示，有一水平桌面长L，套上两端开有小孔的外罩（外罩内情况无法看见），桌面上沿中轴线有一段长度未知的粗糙面，其它部分光滑，一小物块（可视为质点）以速度从桌面的左端沿桌面中轴线方向滑入，小物块与粗糙面的动摩擦系数μ=0.5，小物体滑出后做平抛运动，桌面离地高度h以及水平飞行距离s均为L/2（重力加速度为g）求：

（1）未知粗糙面的长度X为多少？

（2）若测得小物块从进入桌面到落地经历总时间为，则粗糙面的前端离桌面最左端的距离？

（3）粗糙面放在何处，滑块滑过桌面用时最短，该时间为多大？

Answer 1

【答案】（1）L/4 （2）（3）

【解析】

试题分析：(1)平抛运动：

牛顿第二定律：

水平方向直线运动：v2-v02=-2ax

（或用动能定理：

解得：x=L/4

（2）令粗糙面的前端离桌面最左端距离为d,已知x=L/4，且不管粗糙面放哪，末速度不变为，但运行时间不同。

匀速直线运动

匀减速直线运动

匀速直线运动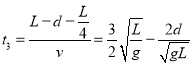

平抛运动：

由,解得：

（3）不管粗糙面放哪，末速度不变为，由第（2）小题知：t2不变，两段匀速直线运动，总位移为，且v＜v0，让大速度v0位移最长时，运行时间最短，所以粗糙面前端应放在离桌面最左端处．

匀速直线运动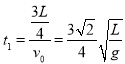；匀减速直线运动

匀速直线运动t3=0，最短时间为