题目内容
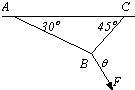AB、BC为两细绳，A、C悬挂于天花板上，B端用一大小恒定的力F拉住，绳与天花板的夹角分别为30°和45°，则要使AB绳所受拉力最大，F与BC间的夹角θ 应为（ ）分析：结B点受到三个拉力而平衡，故将拉力F沿着平行AB和BC方向分解，可得AB绳所受拉力最大对应的θ值．
解答：解：结B点受到三个拉力而平衡，将拉力F沿着平行AB和BC方向分解，如图所示：
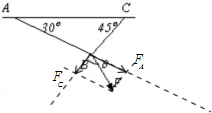
根据平衡条件，有：
=
解得：FA=
F
故当θ=90°时，AB绳所受拉力最大；
故选B．
根据平衡条件，有：
| FA |
| sin(180°-θ) |
| F |
| sin75° |
解得：FA=
| sinθ |
| sin75° |
故当θ=90°时，AB绳所受拉力最大；
故选B．
点评：本题关键对B点受力分析后，根据作用效果将拉力F分解，根据平衡条件求解出AB绳子拉力的表达式进行分析，不难．
练习册系列答案
相关题目
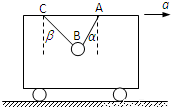
如图，用AB、BC两根细绳把质量为m=1kg的小球悬挂于车内，当小车向右做水平匀速直线运动时，AB绳与竖直方向的夹角为α=37°，BC绳与竖直方向的夹角为β=53°，求：（重力加速度g=10m/s2，sin37°=0.6、cos37°=0.8、sin53°=0.8、cos53°=0.6）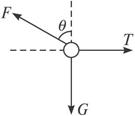
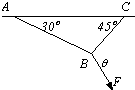AB、BC为两细绳，A、C悬挂于天花板上，B端用一大小恒定的力F拉住，绳与天花板的夹角分别为30°和45°，则要使AB绳所受拉力最大，F与BC间的夹角θ 应为