Question

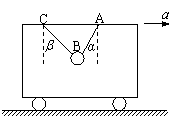
如图，用AB、BC两根细绳把质量为m=1kg的小球悬挂于车内，当小车向右做水平匀速直线运动时，AB绳与竖直方向的夹角为α=37°，BC绳与竖直方向的夹角为β=53°，求：（重力加速度g=10m/s²，sin37°=0.6、cos37°=0.8、sin53°=0.8、cos53°=0.6）
（1）两细绳的张力大小；
（2）当小车以a=8m/s²的加速度向右水平行驶时，两绳的张力．

Answer 1

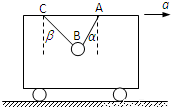
【答案】分析：（1）小车匀速运动，小球处于平衡状态，对小球进行受力分析，根据平衡条件列式即可求解；
（2）当小车向右加速水平行驶时，小球可能会飘起，先求出临界加速度，比较给定的加速度与临界加速度的关系根据牛顿第二定律即可求解．
解答：解：（1）对小球进行受力分析，根据平衡条件得：
T₂sinβ=T₁sinα，
T₂cosβ+T₁cosα=mg
解得T₁=8N，T₂=6N．
（2）当小车加速时有可能小球飘起，临界加速度为a，
mg tanα=ma，
a=7.5m/s²，
现a＞a，故小球飘起，BC不受力，
Fsinα′=ma，
Fcosα′=mg，
tanα′=0.8，
F=12.8N
答：（1）两细绳的张力大小分别为8N和6N；
（2）当小车以a=8m/s²的加速度向右水平行驶时，BC绳的张力为零，AB绳的张力为12.8N．
点评：本题主要考查了同学们能力分析的能力，根据平衡条件及牛顿第二定律列式求解，难度适中．