题目内容
【题目】如图所示，在一直立的光滑管内放置一轻质弹簧，管口上方O点与弹簧上端初始位置A的距离为h，一小球从O点由静止下落，压缩弹簧至最低点D，弹簧始终处于弹性限度内，不计空气阻力，小球自O点下落到最低点D的过程中，下列说法正确的是（ ）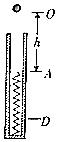
A.小球与弹簧组成的系统机械能守恒
B.小球的最大速度与h无关
C.小球达到最大速度的位置随h的变化而变化
D.弹簧的最大弹性势能与h成正比
【答案】A
【解析】解：A、小球在运动的过程中只有重力和弹簧的弹力做功，小球与弹簧组成的系统机械能守恒．A符合题意；
B、设小球刚运动到A点时的速度为v，则有mgh= 
mv2，v= 
．小球接触弹簧后先做加速运动．
当弹簧的弹力与重力大小相等时，弹簧压缩量为x，此时小球的速度最大；则有mg=kx，x= 
．
该过程中机械能守恒，由功能关系可得： 
得： 
，可知小球的最大速度与h有关．B不符合题意；
C、当弹簧的弹力与重力大小相等时，即弹簧压缩量为 时小球的速度最大，与h无关，C不符合题意；
D、选取小球的平衡位置处为重力势能的0点，当小球运动到最低点D时，弹性势能最大，动能为0，则弹簧的弹性势能等于取小球的平衡位置处小球与弹簧组成的系统的机械能．
根据机械能守恒定律得，弹簧的最大弹性势能为： 
= 
，可知弹簧的最大弹性势能与h是线性关系，但不是成正比．D不符合题意．
答案为：A
【考点精析】通过灵活运用机械能综合应用，掌握系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、
练习册系列答案
相关题目
