题目内容
【题目】如图,地球半径为R.地球表面的重力加遠度为g,离地面高h的轨道上有两颗卫星1和2,若两颗卫星地球逆时针做匀速圆周运动,不计两卫星间的相互作用力,则
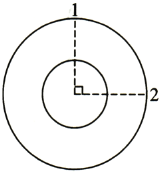
A. 若卫星2向后喷气就一定能追上卫星1
B. 由2位置运动到1位置过程中引力做正功
C. 这两颗卫星的加速度大小相等,均为![]()
D. 由2位置运动到1位置经历的时间是![]()
【答案】CD
【解析】
两卫星处于同一轨道上,加速度大小相等,两卫星均由由万有引力提供向心力,由牛顿第二定律得到加速度与半径的关系.卫星2向后喷气将做离心运动,轨道半径增大,不可能追上卫星.由卫星的速度公式求出其角速度,即可求出卫星1由位置2第一次运动到位置1所用的时间.卫星由位置2运动到位置1的过程中,万有引力与速度总是垂直,不做功.
两卫星在同一轨道上,卫星2向后喷气线速度增大,将做离心运动,轨道半径增大,不可能追上卫星1.故A错误。卫星由位置2运动到位置1的过程中,万有引力与速度总是垂直,不做功,故B错误。在地球表面上,有![]() ,在运行轨道上有:
,在运行轨道上有:![]() ,联立解得:
,联立解得:![]() ,故C正确;运动经历的时间
,故C正确;运动经历的时间![]() ,且
,且![]() 。所以
。所以![]() ,故D正确;故选CD。
,故D正确;故选CD。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目